有七种颜色的珍珠，共计 $14$ 颗，其中每种颜色的珍珠各两颗；今把这些珍珠分装于七个珠盒中，使得每个珠盒中各有一对不同颜色的珍珠．
【难度】
【出处】
2009年全国高中数学联赛山西省预赛
【标注】
-
证明：不论各盒中的珍珠怎样搭配，总可以将这七个珠盒分别放置于一个正七边形的七个顶点之上，使得七边形的任两个相邻顶点处所放置的盒中的四颗珍珠互不同色；标注答案略解析用点 $v_1,v_2,\cdots ,v_7$ 分别表示这七种颜色，如果一个 $v_i$ 色的珍珠和一个 $v_j$ 色的珍珠装在同一盒中（$i\ne j$），则在点 $v_i$ 与 $v_j$ 间连一条边，这样就得到一个图 $G$（点 $v_i$ 与 $v_j$ 之间有可能连出两条边）．
由于同一色的珍珠有两颗，每颗珍珠都需与一颗其他颜色的珍珠共盒，则图 $G$ 的每点恰好发出两条边；从 $G$ 的任一点 $A$ 出发，沿一条边走到点 $B$，再由 $B$ 沿另一条边走到 $C\cdots $ 如此下去，最后必定回到出发点 $A$（这是由于，途中经过的每个点 $P$ 都有两条边，若能沿一条边进入点 $P$，则必沿另一条边可离开点 $P$，而由点 $P$ 不能再回到途中已经过的点，因为这种点所发出的两条边都已走过，因此只能到达新点或回到出发点，而新点终将逐渐耗尽，最后必定回到出发点 $A$），这样就得到一个圈．
去掉这个圈，若剩下还有点，依上述方法，又将得到新的圈，若称两点的圈为“两边形”，则图 $G$ 的结构只有如下四种情况：情形一 一个七边形：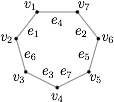
情形二 一个五边形和一个两边形：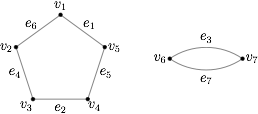
情形三 一个四边形和一个三角形：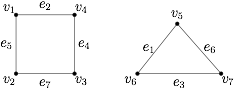
情形四 一个三角形和两个两边形：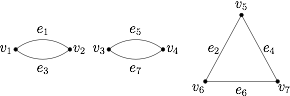
对于每种情况，我们都对对应的边作出适当编号，并将这些边所对应的珠盒放置于七边形的顶点之上，如图所示：
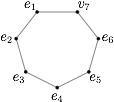因此所证结论成立． -
如将以上条件与待证结论中的“七”一律改为“五”，“$14$”改为“$10$”，则情况如何？标注答案结论不成立解析当 $14$ 颗七色珍珠改为 $10$ 颗五色珍珠后，结论不成立．
例如，对于五色 $v_1,v_2,v_3,v_4,v_5$，我们若将 $10$ 颗珍珠这样装盒：$$e_1=(v_1,v_2),e_2=(v_2,v_3),e_3=(v_3,v_1),e_4=(v_4,v_5),e_5=(v_4,v_5),$$则无论怎样摆放于正五边形的顶点上，都不能满足条件（因为 $e_1,e_2,e_3$ 中，任两盒都有同色的珍珠，无论怎样摆放于正五边形的顶点上，必有两盒相邻）．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
