设正整数 $n\geqslant 2$，对 $2\times n$ 格点链中的 $2n$ 个结点用红（$R$），黄（$Y$），蓝（$B$）三种颜色染色，左右端点中的三个结点已经染好色，如图所示．若对剩余的 $2n-3$ 个结点，要求每个结点恰染一种颜色，相邻结点异色，求不同的染色方法数．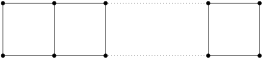
【难度】
【出处】
2016年全国高中数学联赛浙江省预赛（二试）
【标注】
【答案】
$3^{n-1}$
【解析】
对 $2\times n$ 格点链中的 $2n$ 个结点用红（$R$），黄（$Y$），蓝（$B$）三种颜色染色，其中左端点染红色与黄色，设右端点染色为 $P,Q$，如图1所示．
记 $P=R$（或 $Y$），$Q=B$ 时的着色数目为 $a_{n}$；记 $P=B,Q=R$（或 $Y$）时的着色数目为 $b_{n}$；记 $P=R$，$Q=Y$ 或者 $P=Y$，$Q=R$ 时的着色数目为 $c_{n}$．
如图2，我们注意到：
若右端没有约束时，每增加一个格点都有 $3$ 种不同的着色方法，则\[a_{n}+b_{n}+c_{n}=3^{n-1}.\]由对称性，将图形上下翻转，并且颜色 $R$ 和 $Y$ 互换，可知 $a_{n}=b_{n}$．
考虑相互递推的特征，则\[a_{n}=2b_{n-1}+c_{n-1}.\]因此$$\begin{cases}a_{n}+b_{n}+c_{n}=3^{n-1},\\ a_{n}=b_{n},\\ a_{n}=2b_{n-1}+c_{n-1}.\end{cases},n\in\mathbb N^{*}$$这样，\[a_{n}=2b_{n-1}+c_{n-1}=a_{n-1}+b_{n-1}+c_{n-1}=3^{n-1},\]故不同的染色方法数为 $3^{n-1}$．
记 $P=R$（或 $Y$），$Q=B$ 时的着色数目为 $a_{n}$；记 $P=B,Q=R$（或 $Y$）时的着色数目为 $b_{n}$；记 $P=R$，$Q=Y$ 或者 $P=Y$，$Q=R$ 时的着色数目为 $c_{n}$．如图2，我们注意到：
若右端没有约束时，每增加一个格点都有 $3$ 种不同的着色方法，则\[a_{n}+b_{n}+c_{n}=3^{n-1}.\]由对称性，将图形上下翻转，并且颜色 $R$ 和 $Y$ 互换，可知 $a_{n}=b_{n}$．考虑相互递推的特征，则\[a_{n}=2b_{n-1}+c_{n-1}.\]因此$$\begin{cases}a_{n}+b_{n}+c_{n}=3^{n-1},\\ a_{n}=b_{n},\\ a_{n}=2b_{n-1}+c_{n-1}.\end{cases},n\in\mathbb N^{*}$$这样，\[a_{n}=2b_{n-1}+c_{n-1}=a_{n-1}+b_{n-1}+c_{n-1}=3^{n-1},\]故不同的染色方法数为 $3^{n-1}$．
答案
解析
备注
