如图在平面直角坐标系 $xOy$ 中，菱形 $ABCD$ 的边长为 $4$，且 $|OB|=|OD|=6$．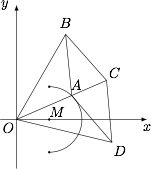
【难度】
【出处】
2012年全国高中数学联赛（一试）
【标注】
-
求证：$|OA|\cdot|OC|$ 为定值；标注答案略解析因为$$|OB|=|OD| , |AB|=|AD|=|CB|=|CD|,$$所以 $O,A,C$ 三点共线．
如图．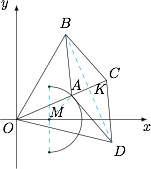
连接 $BD$，则 $BD$ 垂直平分线段 $AC$，设垂足为 $K$，于是有\[\begin{split}|OA|\cdot|OC|&=(|OK|-|AK|)(|OK|+|AK|)\\&=|OK|^2-|AK|^2\\&=(|OB|^2-|BK|^2)-(|AB|^2-|BK|^2)\\&=|OB|^2-|AB|^2\\&=20.\end{split}\] -
当点 $A$ 在半圆 $M:(x-2)^2+y^2=4(2\leqslant x\leqslant4)$ 上运动时，求点 $C$ 的轨迹．标注答案点 $C$ 的轨迹是一条线段，其两个端点的坐标分别为 $(5,5)$，$(5,-5)$解析设 $C(x,y),A(2+2\cos\alpha,2\sin\alpha)$，其中$$\alpha=\angle XMA\left(-\dfrac{\pi}{2}\leqslant\alpha\leqslant\dfrac{\pi}{2}\right),$$则 $\angle XOC=\dfrac{\alpha}{2}$．
因为$$\begin{split}|OA|^2&=(2+2\cos\alpha)^2+(2\sin\alpha)^2\\&=8(1+\cos\alpha)\\&=16\cos^2\dfrac{\alpha}{2},\end{split}$$所以 $|OA|=4\cos\dfrac{\alpha}{2}$．
由 $(1)$ 的结论，得 $|OC|\cos\dfrac{\alpha}{2}=5$，所以$$x=|OC|\cos\dfrac{\alpha}{2}=5,$$从而$$y=|OC|\sin\dfrac{\alpha}{2}=5\tan\dfrac{\alpha}{2}\in[-5,5],$$故点 $C$ 的轨迹是一条线段，其两个端点的坐标分别为 $(5,5)$，$(5,-5)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
