从区间 $\left[0,1\right]$ 随机抽取 $2n$ 个数 $x_1,x_2,\cdots,x_n,y_1,y_2,\cdots ,y_n,$ 构成 $n$ 个数对 $\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots,\left(x_n,y_n\right)$，其中两数的平方和小于 $1$ 的数对共有 $m$ 个，则用随机模拟的方法得到的圆周率 ${\mathrm \pi} $ 的近似值为 \((\qquad)\)
【难度】
【出处】
2016年高考全国甲卷（理）
【标注】
【答案】
C
【解析】
本题主要考查几何概型，由题意列出含 ${\mathrm \pi} $ 的等式即可．由题意得，$\left( {{x}_{i}} {{y}_{i}} \right)\left( i=1 , 2 , \cdot \cdot \cdot , n \right)$ 在如图所示方格中，而平方和小于1的点均在如图所示的阴影中．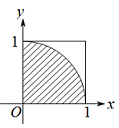
由几何概型概率计算公式知 $\dfrac{\frac{\mathrm \pi} {4}}{1}=\dfrac{m}{n}$，所以 $ {\mathrm \pi} =\dfrac{4m}{n}$，故选C．
由几何概型概率计算公式知 $\dfrac{\frac{\mathrm \pi} {4}}{1}=\dfrac{m}{n}$，所以 $ {\mathrm \pi} =\dfrac{4m}{n}$，故选C．
题目
答案
解析
备注
