假设平面点集 $S$ 具有性质：（i）任意三点不共线；（ii）任意两点距离各不相等．对于 $S$ 中两点 $A,B$，若存在 $C\in S$ 使得 $|AC|<|AB|<|BC|$，则称 $AB$ 是 $S$ 的一条中边．对于 $S$ 中三点 $A,B,C$，若 $AB,AC,BC$ 都是 $S$ 的中边，则称 $\triangle{ABC}$ 是 $S$ 的中边三角形．求最小的 $n$ 使得任意具有性质（i）和（ii）的 $n$ 元平面点集 $S$ 中一定存在中边三角形．
【难度】
【出处】
2009年全国高中数学联赛安徽省预赛
【标注】
【答案】
$6$
【解析】
将 $S$ 的所有中边染成红色，其他边染成蓝色．
当 $n\geqslant 6$ 时，根据Ramsey定理，一定存在同色三角形，该三角形一定有中边，一定是中边三角形．
存在具有性质（i）（ii）的 $5$ 元点集，但是它没有中边三角形，例如：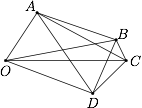
其中 $AB,OB,OD$ 为三条中边，但不能组成三角形．
当 $n\geqslant 6$ 时，根据Ramsey定理，一定存在同色三角形，该三角形一定有中边，一定是中边三角形．
存在具有性质（i）（ii）的 $5$ 元点集，但是它没有中边三角形，例如：
其中 $AB,OB,OD$ 为三条中边，但不能组成三角形．
答案
解析
备注
