如图所示,已知 $A,B,C$ 是长轴长为 $4$ 的椭圆上的三点,点 $A$ 是长轴的一个端点,$BC$ 过椭圆中心 $O$,且 $\overrightarrow{AC}\cdot\overrightarrow{BC}=0$,$|BC|=2|AC|$.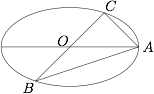

【难度】
【出处】
2008年全国高中数学联赛黑龙江省预赛
【标注】
-
建立适当的坐标系,求椭圆方程;标注答案$\dfrac{x^2}{4}+\dfrac{3y^2}{4}=1$解析以 $O$ 为原点,$OA$ 为 $x$ 轴建立直角坐标系.
设 $A(2,0)$,则椭圆方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{b^2}=1$,$O$ 为椭圆中心.
由对称性知 $|OC|=|OB|$,结合 $\overrightarrow{AC}\cdot\overrightarrow{BC}=0$,可知 $AC\perp BC$.
结合 $|BC|=2|AC|$,则 $|OC|=|AC|$,因此 $\triangle AOC$ 为等腰直角三角形,易得点 $C$ 的坐标为 $(1,1)$,点 $B$ 的坐标为 $(-1,1)$,代入椭圆,得 $b^2=\dfrac43$,故方程为$$\dfrac{x^2}{4}+\dfrac{3y^2}{4}=1.$$ -
如果椭圆上有两点 $P,Q$,使 $\angle PCQ$ 的平分线垂直于 $AO$,证明:存在实数 $\lambda$,使得 $\overrightarrow{PQ}=\lambda\overrightarrow{AB}$.标注答案略解析由于 $\angle PCQ$ 的平分线垂直于 $OA$,不妨设 $PC$ 的斜率为 $k$,则 $QC$ 的斜率为 $-k$,因此 $PC,QC$ 的直线方程分别为$$y=k(x-1)+1 , y=-k(x-1)+1.$$联立 $PC$ 与椭圆,得$$(1+3k^2)x^2-6k(k-1)x+3k^2-6k-1=0.$$因为点 $C(1,1)$ 在椭圆上,所以 $x=1$ 是上述方程的一个根,则$$x_P=\dfrac{3k^2-6k-1}{3k^2+1}.$$同理可得$$x_Q=\dfrac{3k^2-6k-1}{3k^2+1}.$$因此直线 $PQ$ 的斜率为$$\dfrac{y_P-y_Q}{x_P-x_Q}=\dfrac{k(x_P+x_Q)-2k}{x_P-x_Q}=\dfrac13.$$易求得 $K_{AB}=\dfrac13$,因此 $\overrightarrow{PQ}\parallel\overrightarrow{AB}$,即总存在实数 $\lambda$,使得 $\overrightarrow{PQ}=\lambda\overrightarrow{AB}$ 成立.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2