已知正三棱柱 $ABC-A_1B_1C_1$ 中，$AA_1=2AC=4$，延长 $CB$ 至 $D$，使 $CB=BD$．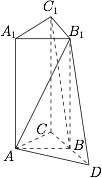
【难度】
【出处】
2008年全国高中数学联赛贵州省预赛
【标注】
-
求证：直线 $C_1B\parallel\text{平面}AB_1D$；标注答案略解析连接 $C_1B$，则$$C_1B_1=CB=DB.$$又因为 $C_1B_1\parallel BD$，所以四边形 $C_1BDB_1$ 是平行四边形，从而$$C_1B\parallel B_1D.$$又因为 $B_1D\subset\text{平面}AB_1D$，所以直线 $C_1B\parallel\text{平面}AB_1D$．
-
求平面 $AB_1D$ 与平面 $ACB$ 所成角的正弦值．标注答案$\dfrac{4\sqrt{17}}{17}$解析在 $\triangle ACD$ 中，由于$$CB=BD=BA,$$故 $\angle DAC=90^\circ$．
以 $A$ 为原点，建立如图空间直角坐标系．
因为 $A(0,0,0),B_1(\sqrt3,1,4),D(2\sqrt3,0,0)$，所以$$\overrightarrow{AD}=\left(2\sqrt3,0,0\right),\overrightarrow{AB_1}=\left(\sqrt3,1,4\right).$$设平面 $AB_1D$ 的法向量 $\overrightarrow{n}=(x,y,z)$，则$$\begin{cases}\overrightarrow{n}\cdot\overrightarrow{AD}=0,\\ \overrightarrow{n}\cdot\overrightarrow{AB_1}=0,\end{cases}$$即$$\begin{cases}2\sqrt3x=0,\\ \sqrt3x+y+4z=0,\end{cases}$$令 $z=1$，则 $\overrightarrow{n}=(0,-4,1)$．
取平面 $ACB$ 的法向量为 $\overrightarrow{m}=(0,0,1)$，则$$\cos\left\langle\overrightarrow{n},\overrightarrow{m}\right\rangle=\dfrac{\overrightarrow{n}\cdot\overrightarrow{m}}{\left|\overrightarrow{n}\right|\left|\overrightarrow{m}\right|}=\dfrac{1}{\sqrt{17}},$$所以$$\sin\left\langle\overrightarrow{n},\overrightarrow{m}\right\rangle=\dfrac{4\sqrt{17}}{17}.$$因此，平面 $AB_1D$ 和平面 $ACB$ 所成角的正弦值为 $\dfrac{4\sqrt{17}}{17}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
