已知 $ a,b\in \mathbb R $,$ 1 $ 和 $ -1 $ 是函数 $ f\left(x\right)=x^3+ax^2+bx $ 的两个极值点.
【难度】
【出处】
无
【标注】
-
求 $ a $ 和 $ b $ 的值;标注答案$a=0,b=-3$解析$f(x)$ 的导函数$$f'(x)=3x^2+2ax+b,$$由韦达定理得 $a=0,b=-3$.
-
设函数 $ g\left(x\right) $ 的导函数 $ g'\left(x\right)=f\left(x\right)+2 $,求 $ g\left(x\right) $ 的极值点;标注答案$x=2$解析根据题意,有$$g'(x)=x^3-3x+2=(x-1)^2(x-2),$$于是 $g(x)$ 的极值点为 $x=2$.
-
设 $h\left(x\right)=f\left(f\left(x\right)\right)-c$,其中 $c\in \left[-2,2\right]$,求函数 $y=h\left(x\right)$ 的零点个数.标注答案$9$解析函数 $f(x)$ 的图象如图.
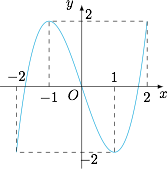
情形一 当 $c=\pm 2$ 时,零点个数为 $5$.情形二 当 $-2<c<2$ 时,零点个数为 $9$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3