已知 $\triangle{ABC}$ 的内切圆半径为 $2$，且 $\tan A=-\dfrac 43$，求 $\triangle{ABC}$ 面积的最小值．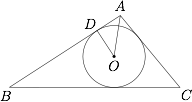
【难度】
【出处】
2009年全国高中数学联赛新疆维吾尔自治区预赛
【标注】
【答案】
$18+8\sqrt 5$
【解析】
设 $AB=c$，$BC=a$，$AC=b$，$D$ 为切点，可知$$2AD+2a=a+b+c,$$所以$$AD=\dfrac 12(b+c-a).$$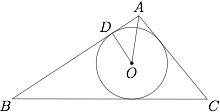
由 $\tan A=-\dfrac 43$ 可得 $\tan{\angle{DAO}}=2$，所以$$DO=2AD=b+c-a=2.$$又 $\sin A=\dfrac 45$，故$$S_{\triangle{ABC}}=\dfrac 12bc\sin A=\dfrac 25 bc.$$又因为$$S_{\triangle{ABC}}=\dfrac 12(a+b+c)\cdot 2,$$所以$$\dfrac 25 bc=a+b+c=2(b+c)-2,$$故$$bc=5(b+c)-5\geqslant 10\sqrt{bc}-5,$$于是$$bc-10\sqrt{bc}+5\geqslant 0,$$从而 $\sqrt{bc}\geqslant 5+2\sqrt 5$，即 $bc\geqslant 45+20\sqrt 5$，因此$$S_{\triangle{ABC}}=\dfrac 25 bc\geqslant 18+8\sqrt 5,$$当 $b=c=5+2\sqrt 5$ 时取得等号．
因此 $\triangle{ABC}$ 面积的最小值为 $18+8\sqrt 5$．
由 $\tan A=-\dfrac 43$ 可得 $\tan{\angle{DAO}}=2$，所以$$DO=2AD=b+c-a=2.$$又 $\sin A=\dfrac 45$，故$$S_{\triangle{ABC}}=\dfrac 12bc\sin A=\dfrac 25 bc.$$又因为$$S_{\triangle{ABC}}=\dfrac 12(a+b+c)\cdot 2,$$所以$$\dfrac 25 bc=a+b+c=2(b+c)-2,$$故$$bc=5(b+c)-5\geqslant 10\sqrt{bc}-5,$$于是$$bc-10\sqrt{bc}+5\geqslant 0,$$从而 $\sqrt{bc}\geqslant 5+2\sqrt 5$，即 $bc\geqslant 45+20\sqrt 5$，因此$$S_{\triangle{ABC}}=\dfrac 25 bc\geqslant 18+8\sqrt 5,$$当 $b=c=5+2\sqrt 5$ 时取得等号．因此 $\triangle{ABC}$ 面积的最小值为 $18+8\sqrt 5$．
答案
解析
备注
