查看数据源：599165c82bfec200011e1595
如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是 $\dfrac{28{\mathrm \pi} }{3}$，则它的表面积是 \((\qquad)\)  
A: $17{\mathrm \pi} $
B: $18{\mathrm \pi} $
C: $20{\mathrm \pi} $
D: $28{\mathrm \pi} $
【难度】
【出处】
2016年高考全国乙卷（文）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
  • 题型
    >
    立体几何
【答案】
A
【解析】
本题考查球体的三视图问题，关键在于想象出球体中缺少的部分在球体的左上角．原立体图如图所示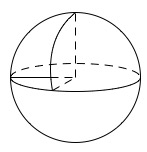： 该图是一个球被切掉左上角的 $\dfrac18$ 后的图形，表面积是 $\dfrac78$ 的球面面积和三个扇形面积之和，即\[S=\dfrac78\cdot4{\mathrm \pi} \cdot2^2+3\cdot\dfrac14{\mathrm \pi} \cdot2^2=17{\mathrm \pi} .\]
题目 答案 解析 备注
0.109831s