将 $33\times 33$ 方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等．若相邻两个小方格的颜色不同，则称它们的公共边为“分隔边”．试求分隔边条数的最小值．
【难度】
【出处】
2017年全国高中数学联赛A卷（二试）
【标注】
【答案】
$56$
【解析】
如图，分隔边的条数 $L=56$．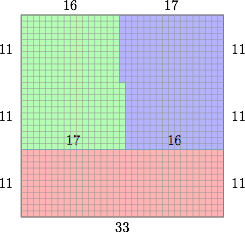
下面证明 $L\geqslant 56$．将方格纸的行从上至下依次记为 $A_1,A_2,\cdots,A_{33}$，列从左至右依次记为 $B_1,B_2,\cdots,B_{33}$．行 $A_i$ 中方格出现的颜色数记为 $n(A_i)$，列 $B_i$ 中方格出现的颜色数记为 $n(B_i)$，三种颜色分别记为 $c_1,c_2,c_3$，对于一种颜色 $c_j$，设 $n(c_j)$ 是含有 $c_j$ 色方格的行数与列数之和．若 $A_i$ 行中含有 $c_j$ 色的方格，则记 $\delta(A_i,c_j)$ 为 $1$，否则记 $\delta(A_i,c_j)$ 为 $0$．类似的定义 $\delta(B_i,c_j)$，于是\[\begin{split}\sum_{i=1}^{33}\left(n(A_i)+n(B_i)\right)
&=\sum_{i=1}^{33}\sum_{j=1}^3\left(\delta(A_i,c_j)+\delta(B_i,c_j)\right)\\
&=\sum_{j=1}^3\sum_{i=1}^{33}\left(\delta(A_i,c_j)+\delta(B_j,c_j)\right)\\
&=\sum_{j=1}^3n(c_j),\end{split}\]由于染 $c_j$ 色的方格数为\[\dfrac 13\cdot 33^2=363,\]设含有 $ c_j $ 色方格的行有 $ a $ 个，列有 $ b $ 个，则 $ c_j $ 色方格一定在这 $ a $ 行和 $ b $ 列的交叉方格中，因此\[ab\geqslant 363,\]从而\[n(c_j)=a+b\geqslant 2\sqrt{ab}>2\sqrt{363}>38,\]故\[n(c_j)\geqslant 39,j=1,2,3.\]由于在行 $ A_i $ 中有 $ n(A_i)$ 种颜色的方格，因此至少有 $ n(A_i)-1 $ 条分割边，同理在列 $ B_i $ 中，至少有 $ n(B_i)-1$ 条分割边，于是\[\begin{split}L&\geqslant \sum_{i=1}^{33}\left(n(A_i)-1\right)+\sum_{i=1}^{33}\left(n(B_i)-1\right)\\
&=\sum_{i=1}^{33}\left(n(A_i)+n(B_i)\right)-66\\
&=\sum_{j=1}^3n(c_j)-66.\end{split}\]下面分两种情形讨论．
情形一 有一行或一列全部方格同色．不妨设有一行全部为 $c_1$ 色，从而方格纸的 $33$ 列中均含有 $c_1$ 色的方格，由于 $c_1$ 色方格有 $363$ 个，故至少有 $11$ 行中含有 $c_1$ 色方格，于是\[n(c_1)\geqslant 11+33=44,\]于是\[L\geqslant n(c_1)+n(c_2)+n(c_3)-66\geqslant 44+39+39-66=56.\]情形二 没有一行也没有一列的全部方格同色，则对任意 $1\leqslant i\leqslant 33$，具有 $n(A_i)\geqslant 2$，$n(B_i)\geqslant 2$，从而可得\[L\geqslant \sum_{i=1}^{33}\left(n(A_i)+n(B_i)\right)-66\geqslant 33\cdot 4-66=66.\]综上所述，分隔边条数的最小值为 $56$．
下面证明 $L\geqslant 56$．将方格纸的行从上至下依次记为 $A_1,A_2,\cdots,A_{33}$，列从左至右依次记为 $B_1,B_2,\cdots,B_{33}$．行 $A_i$ 中方格出现的颜色数记为 $n(A_i)$，列 $B_i$ 中方格出现的颜色数记为 $n(B_i)$，三种颜色分别记为 $c_1,c_2,c_3$，对于一种颜色 $c_j$，设 $n(c_j)$ 是含有 $c_j$ 色方格的行数与列数之和．若 $A_i$ 行中含有 $c_j$ 色的方格，则记 $\delta(A_i,c_j)$ 为 $1$，否则记 $\delta(A_i,c_j)$ 为 $0$．类似的定义 $\delta(B_i,c_j)$，于是\[\begin{split}\sum_{i=1}^{33}\left(n(A_i)+n(B_i)\right)&=\sum_{i=1}^{33}\sum_{j=1}^3\left(\delta(A_i,c_j)+\delta(B_i,c_j)\right)\\
&=\sum_{j=1}^3\sum_{i=1}^{33}\left(\delta(A_i,c_j)+\delta(B_j,c_j)\right)\\
&=\sum_{j=1}^3n(c_j),\end{split}\]由于染 $c_j$ 色的方格数为\[\dfrac 13\cdot 33^2=363,\]设含有 $ c_j $ 色方格的行有 $ a $ 个，列有 $ b $ 个，则 $ c_j $ 色方格一定在这 $ a $ 行和 $ b $ 列的交叉方格中，因此\[ab\geqslant 363,\]从而\[n(c_j)=a+b\geqslant 2\sqrt{ab}>2\sqrt{363}>38,\]故\[n(c_j)\geqslant 39,j=1,2,3.\]由于在行 $ A_i $ 中有 $ n(A_i)$ 种颜色的方格，因此至少有 $ n(A_i)-1 $ 条分割边，同理在列 $ B_i $ 中，至少有 $ n(B_i)-1$ 条分割边，于是\[\begin{split}L&\geqslant \sum_{i=1}^{33}\left(n(A_i)-1\right)+\sum_{i=1}^{33}\left(n(B_i)-1\right)\\
&=\sum_{i=1}^{33}\left(n(A_i)+n(B_i)\right)-66\\
&=\sum_{j=1}^3n(c_j)-66.\end{split}\]下面分两种情形讨论．
答案
解析
备注
