已知 $P$ 为三角形 $ABC$ 的费马点，记 $PA$，$PB$，$PC$ 的长为 $x$，$y$，$z$，三角形的边长为 $a$，$b$，$c$．求证：\[(x+y+z)^2\leqslant ab+bc+ca.\]
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图，将 $\triangle APC$ 旋转 $60^\circ$ 到 $\triangle EDC$．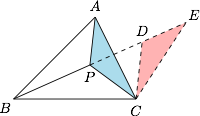
有\[\begin{split}(x+y+z)^2&=a^2+b^2-2ab\cos\left(C+\frac{\pi}3\right)\\ &=a^2+b^2-2ab\left(\frac 12\cos C-\frac{\sqrt 3}2\sin C\right)\\ &=a^2+b^2-2ab\left(\frac{a^2+b^2-c^2}{4ab}-\frac{\sqrt 3}2\cdot\frac{\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^2}}{2ab}\right).\end{split}\]整理，得原不等式等价于\[\left(2\sum_{cyc}ab-\sum_{cyc}a^2\right)^2\geqslant 3\left(2\sum_{cyc}a^2b^2-\sum_{cyc}a^4\right).\]该不等式即\[\sum_{cyc}\left(a^4-ab^2c\right)\geqslant\sum_{cyc}\left(a^3b+ab^3\right).\]此即Schur不等式当 $r=2$ 时的情形．
有\[\begin{split}(x+y+z)^2&=a^2+b^2-2ab\cos\left(C+\frac{\pi}3\right)\\ &=a^2+b^2-2ab\left(\frac 12\cos C-\frac{\sqrt 3}2\sin C\right)\\ &=a^2+b^2-2ab\left(\frac{a^2+b^2-c^2}{4ab}-\frac{\sqrt 3}2\cdot\frac{\sqrt{4a^2b^2-\left(a^2+b^2-c^2\right)^2}}{2ab}\right).\end{split}\]整理，得原不等式等价于\[\left(2\sum_{cyc}ab-\sum_{cyc}a^2\right)^2\geqslant 3\left(2\sum_{cyc}a^2b^2-\sum_{cyc}a^4\right).\]该不等式即\[\sum_{cyc}\left(a^4-ab^2c\right)\geqslant\sum_{cyc}\left(a^3b+ab^3\right).\]此即Schur不等式当 $r=2$ 时的情形．
答案
解析
备注
