是否存在五棱锥 $P-ABCDE$，使得它的五个侧面都是直角三角形？如果存在，构造一个各侧面都是直角三角形的五棱锥 $P-ABCDE$．如果不存在，说明理由．
【难度】
【出处】
2009年第二十届“希望杯”全国数学邀请赛高一（二试）
【标注】
【答案】
存在
【解析】
存在．如图，平面上 $\triangle ADE,\triangle ACD,\triangle ACB$ 均为直角三角形，且\[\angle BAC=\angle CAD=\angle DAE=30^\circ.\]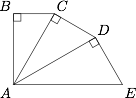
过点 $A$ 作平面 $ABCDE$ 的垂线，在垂线上任取不同于点 $A$ 的点 $P$，则显然侧面 $PAE,PAB$ 均为直角三角形，又\[\begin{cases} CB\perp AB,\\ CB\perp AP,\end{cases} \Rightarrow CB\perp ABP\Rightarrow CB\perp PB,\]于是侧面 $PBC$ 也是直角三角形．类似的，可得侧面 $PCD,PDE$ 为直角三角形，因此五棱锥 $P-ABCDE$ 的 $5$ 个侧面均为直角三角形，结论得证．
过点 $A$ 作平面 $ABCDE$ 的垂线，在垂线上任取不同于点 $A$ 的点 $P$，则显然侧面 $PAE,PAB$ 均为直角三角形，又\[\begin{cases} CB\perp AB,\\ CB\perp AP,\end{cases} \Rightarrow CB\perp ABP\Rightarrow CB\perp PB,\]于是侧面 $PBC$ 也是直角三角形．类似的，可得侧面 $PCD,PDE$ 为直角三角形，因此五棱锥 $P-ABCDE$ 的 $5$ 个侧面均为直角三角形，结论得证．
答案
解析
备注
