设 $x_1,x_2,\cdots,x_{100}\in [-1,1]$，求证：存在 $i\ne j$ 使得 $|x_ix_{j+1}-x_jx_{i+1}|<\dfrac{1}{12}$．
【难度】
【出处】
2016年中国科学技术大学优秀中学生数学科学营数学试题
【标注】
【答案】
略
【解析】
设坐标平面上 $99$ 个点的坐标分别为 $P_k(x_k,x_{k+1})$（$k=1,2,\cdots,99$）．当这 $99$ 个点包含原点 $O(0,0)$ 时，命题显然成立；否则，将原点与这些点连接，得到射线 $OP_k$．记 $A(1,1)$，$B(-1,1)$，$C(-1,-1)$，$D(1,-1)$，设射线 $OP_k$（$k=1,2,\cdots,99$）与正方形 $ABCD$ 的边分别交于点 $Q_k$（$k=1,2,\cdots,99$）．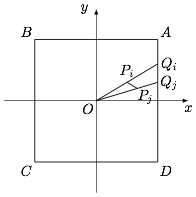
根据抽屉原理，正方形 $ABCD$ 的四条边中至少有一条（记为 $m$，且 $m$ 只包含正方形的一个顶点），它包含 $Q_k$（$k=1,2,\cdots,99$）中不少于 $25$ 个点．这 $25$ 个点必然存在两个点 $Q_i,Q_j$，它们的距离小于 $\dfrac{1}{12}$，于是根据三角形面积坐标公式，记 $\triangle OP_iP_j$ 的面积为 $S_1$（当 $P_i=P_j$ 时，认为面积为 $0$），$\triangle OQ_iQ_j$ 的面积为 $S_2$（当 $Q_i=Q_j$ 时，认为面积为 $0$），则\[|x_ix_{j+1}-x_jx_{i+1}|=2S_1\leqslant 2S_2<\dfrac{1}{12},\]因此原命题得证．
根据抽屉原理，正方形 $ABCD$ 的四条边中至少有一条（记为 $m$，且 $m$ 只包含正方形的一个顶点），它包含 $Q_k$（$k=1,2,\cdots,99$）中不少于 $25$ 个点．这 $25$ 个点必然存在两个点 $Q_i,Q_j$，它们的距离小于 $\dfrac{1}{12}$，于是根据三角形面积坐标公式，记 $\triangle OP_iP_j$ 的面积为 $S_1$（当 $P_i=P_j$ 时，认为面积为 $0$），$\triangle OQ_iQ_j$ 的面积为 $S_2$（当 $Q_i=Q_j$ 时，认为面积为 $0$），则\[|x_ix_{j+1}-x_jx_{i+1}|=2S_1\leqslant 2S_2<\dfrac{1}{12},\]因此原命题得证．
答案
解析
备注
