$c$ 是 $xy=1$ 的图像，$c$ 关于直线 $y=2x$ 的对称图像是 ${c}'$．已知 ${c}'$ 可以写成 $12{{x}^{2}}+bxy+c{{y}^{2}}+d=0$ 的形式，求 $bc$ 的值．
【难度】
【出处】
1988年第6届美国数学邀请赛（AIME）
【标注】
【答案】
84
【解析】
设 $P\left( u v \right)$ 是 $C$ 上任意一点，${P}'\left(x y \right)$ 为 ${C}'$ 上对应的点（即 $P$ 关于 $y=2x$ 的对称点）．连接 $P{P}'$（如图）．因为 $P{P}'\bot $ 直线 $y=2x$，所以 $P{P}'$ 的斜率为 $-\frac{1}{2}$，即 $\frac{y-v}{x-u}=-\frac{1}{2}$．（7）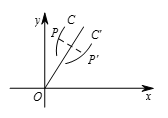
又因为 $P{P}'$ 的中点在 $y=2x$ 上，所以 $\frac{y+v}{2}=2\cdot\frac{x+u}{2}$．（8）
由（7）、（8）得 $u=\frac{4y-3x}{5}$，$v=\frac{4x+3y}{5}$．
把它们代入 $uv=1$，得 $12{{x}^{2}}-7xy-12{{y}^{2}}+25=0$．故 $bc=\left(-7 \right)\left( -12 \right)=84$．
又因为 $P{P}'$ 的中点在 $y=2x$ 上，所以 $\frac{y+v}{2}=2\cdot\frac{x+u}{2}$．（8）由（7）、（8）得 $u=\frac{4y-3x}{5}$，$v=\frac{4x+3y}{5}$．
把它们代入 $uv=1$，得 $12{{x}^{2}}-7xy-12{{y}^{2}}+25=0$．故 $bc=\left(-7 \right)\left( -12 \right)=84$．
答案
解析
备注
