设 $ABCD$ 是一个四面体,且 $AB=41$,$AC=7$,$AD=18$,$BC=36$,$BD=27$,$CD=13$,如图所示,设 $d$ 是棱 $AB$ 和 $CD$ 的中点之间的距离,求 ${{d}^{2}}$.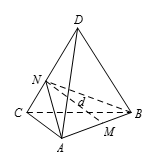

【难度】
【出处】
1989年第7届美国数学邀请赛(AIME)
【标注】
【答案】
137
【解析】
在 $\vartriangle ACD$ 和 $\vartriangle BCD$ 中,根据中线定理可计算
$4A{{N}^{2}}=2\left( A{{C}^{2}}+A{{D}^{2}}\right)-C{{D}^{2}}$,
$4B{{N}^{2}}=2\left( B{{C}^{2}}+B{{D}^{2}}\right)-C{{D}^{2}}$.
同理,连接 $AN$,$BN$,在 $\vartriangle ABN$ 中,
$4{{d}^{2}}=4M{{N}^{2}}=2\left(A{{N}^{2}}+B{{N}^{2}} \right)-A{{B}^{2}}$
$=A{{C}^{2}}+B{{C}^{2}}+A{{D}^{2}}+B{{D}^{2}}-\left(C{{D}^{2}}+A{{B}^{2}} \right)$
$=548$,
${{d}^{2}}=M{{N}^{2}}=137$.
$4A{{N}^{2}}=2\left( A{{C}^{2}}+A{{D}^{2}}\right)-C{{D}^{2}}$,
$4B{{N}^{2}}=2\left( B{{C}^{2}}+B{{D}^{2}}\right)-C{{D}^{2}}$.
同理,连接 $AN$,$BN$,在 $\vartriangle ABN$ 中,
$4{{d}^{2}}=4M{{N}^{2}}=2\left(A{{N}^{2}}+B{{N}^{2}} \right)-A{{B}^{2}}$
$=A{{C}^{2}}+B{{C}^{2}}+A{{D}^{2}}+B{{D}^{2}}-\left(C{{D}^{2}}+A{{B}^{2}} \right)$
$=548$,
${{d}^{2}}=M{{N}^{2}}=137$.
答案
解析
备注