对于正整数 $n$，定义 ${{S}_{n}}$ 为和式 $\displaystyle \sum\limits_{k=1}^{n}{\sqrt{{{\left( 2k-1 \right)}^{2}}+a_{k}^{2}}}$ 的最小值，其中 ${{a}_{1}}$，${{a}_{2}}$，…，${{a}_{n}}$ 为正实数，它们的和为17．已知有唯一的正整数 $n$，使 ${{S}_{n}}$ 也为整数，求 $n$．
【难度】
【出处】
1991年第9届美国数学邀请赛（AIME）
【标注】
【答案】
12
【解析】
把和式中的每一项 ${{t}_{k}}=\sqrt{{{\left( 2k-1 \right)}^{2}}+a_{k}^{2}}$ 看成是以 $2k-1$ 和 ${{a}_{k}}$ 为直角边的直角三角形斜边上的长度．在图中，把这些直角三角形逐个相接形成一个“梯子”，设 $A$，$B$ 是由斜边连接而成的折线的首尾点．$A$，$B$ 的距离为 $\displaystyle \sqrt{{{\left( \sum\limits_{k=1}^{n}{{{a}_{k}}}\right)}^{2}}+{{\left( \sum\limits_{k=1}^{n}{\left( 2k-1 \right)}\right)}^{2}}}=\sqrt{{{17}^{2}}+{{n}^{4}}}$．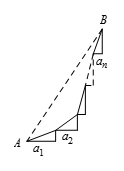
$\displaystyle \sum\limits_{k=1}^{n}{{{t}_{k}}}$ 是从 $A$ 到 $B$ 由斜边连成的折线长度，所以 $\displaystyle \sum\limits_{k=1}^{n}{{{t}_{k}}}\geqslant\sqrt{{{17}^{2}}+{{n}^{4}}}$．选择适当的 ${{a}_{k}}$，可使等号成立，这时折线成为一直线．因此，${{S}_{n}}=\sqrt{{{17}^{2}}+{{n}^{4}}}$ 是可取得的和数的最小值．
当 ${{S}_{n}}$ 是整数时，则 ${{17}^{2}}=S_{n}^{2}-{{n}^{4}}=\left({{S}_{n}}-{{n}^{2}} \right)\left( {{S}_{n}}+{{n}^{2}} \right)$．
由此可推知 $\left\{\begin{align}
& {{S}_{n}}+{{n}^{2}}={{17}^{2}} \\
& {{S}_{n}}-{{n}^{2}}=1. \\
\end{align}\right.$
解这个方程组，得 ${{S}_{n}}=145$，$n=12$．
$\displaystyle \sum\limits_{k=1}^{n}{{{t}_{k}}}$ 是从 $A$ 到 $B$ 由斜边连成的折线长度，所以 $\displaystyle \sum\limits_{k=1}^{n}{{{t}_{k}}}\geqslant\sqrt{{{17}^{2}}+{{n}^{4}}}$．选择适当的 ${{a}_{k}}$，可使等号成立，这时折线成为一直线．因此，${{S}_{n}}=\sqrt{{{17}^{2}}+{{n}^{4}}}$ 是可取得的和数的最小值．当 ${{S}_{n}}$ 是整数时，则 ${{17}^{2}}=S_{n}^{2}-{{n}^{4}}=\left({{S}_{n}}-{{n}^{2}} \right)\left( {{S}_{n}}+{{n}^{2}} \right)$．
由此可推知 $\left\{\begin{align}
& {{S}_{n}}+{{n}^{2}}={{17}^{2}} \\
& {{S}_{n}}-{{n}^{2}}=1. \\
\end{align}\right.$
解这个方程组，得 ${{S}_{n}}=145$，$n=12$．
答案
解析
备注
