在 $\vartriangle ABC$ 中，$AB=13$，$BC=15$ 和 $CA=17$．点 $D$，$E$ 和 $F$ 分别在边 $AB$，$AC$ 和 $CA$ 上．设 $AD=p\cdot AB$，$BE=q\cdot BC$，$CF=r\cdot CA$，其中 $p$，$q$，$r$ 都是正数，且满足 $p+q+r=\frac{2}{3}$，${{p}^{2}}+{{q}^{2}}+{{r}^{2}}=\frac{2}{5}$．$\vartriangle DEF$ 与 $\vartriangle ABC$ 的面积之比可以写成 $\frac{m}{n}$ 的形式，其中 $m$，$n$ 是互素的正整数．求 $m+n$．
【难度】
【出处】
2001年第19届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
61
【解析】
如图所示，用 $\left[ XYZ \right]$ 代表 $\vartriangle XYZ$ 的面积．因为 $p$，$q$，$r$ 都比1小，故
$\left[ BDE\right]=q\left( 1-p \right)\left[ ABC \right]$，
$\left[ EFC\right]=r\left( 1-q \right)\left[ ABC \right]$，
$\left[ ADF\right]=p\left( 1-r \right)\left[ ABC \right]$，
$\left[ ABC\right]=\left[ DEF \right]+\left[ BDE \right]+\left[ EFC \right]+\left[ ADF\right]$
$=\left[ DEF \right]+\left( \left( p+q+r\right)-\left( pq+qr+rp \right) \right)\left[ ABC \right]$
$\frac{\left[DEF \right]}{\left[ ABC \right]}=1+pq+qr+rp-\left( p+q+r \right)$．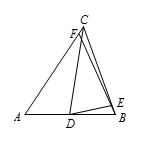
又因为 $pq+qr+rp=\frac{1}{2}\left[{{\left( p+q+r \right)}^{2}}-\left( {{p}^{2}}+{{q}^{2}}+{{r}^{2}} \right)\right]=\frac{1}{2}\left( \frac{4}{9}-\frac{2}{5} \right)=\frac{1}{45}$，
故所求比率为 $1+\frac{1}{45}-\frac{2}{3}=\frac{16}{45}$，所以 $m+n=61$．
$\left[ BDE\right]=q\left( 1-p \right)\left[ ABC \right]$，
$\left[ EFC\right]=r\left( 1-q \right)\left[ ABC \right]$，
$\left[ ADF\right]=p\left( 1-r \right)\left[ ABC \right]$，
$\left[ ABC\right]=\left[ DEF \right]+\left[ BDE \right]+\left[ EFC \right]+\left[ ADF\right]$
$=\left[ DEF \right]+\left( \left( p+q+r\right)-\left( pq+qr+rp \right) \right)\left[ ABC \right]$
$\frac{\left[DEF \right]}{\left[ ABC \right]}=1+pq+qr+rp-\left( p+q+r \right)$．
又因为 $pq+qr+rp=\frac{1}{2}\left[{{\left( p+q+r \right)}^{2}}-\left( {{p}^{2}}+{{q}^{2}}+{{r}^{2}} \right)\right]=\frac{1}{2}\left( \frac{4}{9}-\frac{2}{5} \right)=\frac{1}{45}$，故所求比率为 $1+\frac{1}{45}-\frac{2}{3}=\frac{16}{45}$，所以 $m+n=61$．
答案
解析
备注
