一块圆柱形的木块底面半径为6高为8,其整个表面都被涂上蓝色。点 $A$ 和 $B$ 在同一面的圆周上式的弧 $AB$ 对应圆心角为 $120^\circ $ 。木块被过点 $A$ 和 $B$ 和圆柱中心的平面切成两半,露出两个未被染色的切面。这两个切面的面积均为 $a \cdot \pi + b\sqrt c $,其中 $a,b,c$ 为整数,且 $c$ 不含平方因子。求 $a + b + c$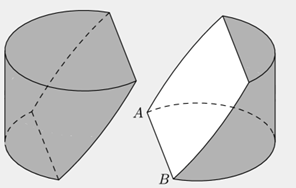

【难度】
【出处】
2015年第33届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
053
【解析】
记平面与顶部圆周交点为 $C,D$,圆柱的中心为 $O$,于是 $C,O,A$ 共线。记 $T$ 为底面圆心,$M$ 为 $AB$ 中点,于是 $OT=4,TM=3$,继而 $OM=5$ 。设 $C,D$ 在底面的竖直投影为 $X,Y$ 。则 $ABCD$ 为 $ABXY$ 的一个拉伸,比值为 $\frac{OM}{TM}=\frac{5}{3}$ 。 $\left[ ABXY \right]=18\sqrt{3}+12\pi $ 。因此 $\left[ ABCD \right]=20\pi +30\sqrt{3}$ 。我们所求的值为 $20+30+3=053$
答案
解析
备注