如图,将同心圆环均匀分成 $n(n\geqslant 3)$ 格,在内环中固定数字 $1\sim n$.问能否将数字 $1\sim n$ 填入外环格内,使得外环旋转任意格后,有且仅有一个格中内外环的数字相同?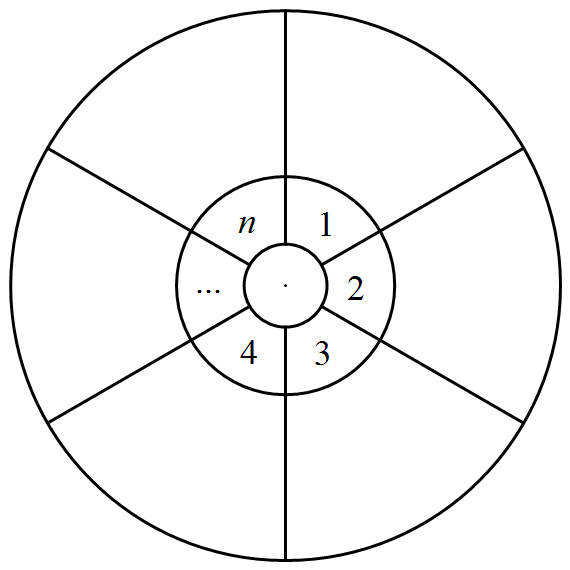

【难度】
【出处】
2018年全国高中数学联赛浙江省预赛
【标注】
【答案】
略
【解析】
设对应于内环 $1,2,\cdots,n$ 的外环数字为 $i_1,i_2,\cdots,i_n$,它是数字 $1,2,\cdots,n$ 的一个排列.对 $k=1,2,\cdots,n$,记外环数字 $i_k$ 在按顺时针方向转动 $j_k$ 格时,和内环数字相同,即 $i_k-k\equiv j_k\pmod{n},k=1,2,\cdots,n$.根据题意,$j_i,j_2,\cdots,j_n$ 应是 $0,1,2,\cdots,n-1$ 的排列.求和 $\displaystyle \sum\limits_{k=1}^{n}{\left( {{i}_{k}}-k\right)\equiv \sum\limits_{k=1}^{n}{{{j}_{k}}\left( \bmod n \right)=\left[0+1+2+\cdots +\left( n-1 \right) \right]}\left( \bmod n \right)=\frac{1}{2}n\left(n-1 \right)}\left( \bmod n \right)$.于是 $n$ 必须是奇数.对于奇数 $n$,我们取 $i_n=n,i_m=n-m,(m=1,2,\cdots,n-1)$,可以验证 ${{i}_{k}}-k\equiv{{j}_{k}}\left( \bmod n \right),\\{{j}_{n}}=0,{{j}_{n-1}}=2,{{j}_{n-2}}=4,\cdots,{{j}_{n-\frac{n-1}{2}}}=n-1,\\{{j}_{1}}=n-2,{{j}_{n-1}}=n-4,{{j}_{3}}=n-6,\cdots,{{j}_{\frac{n-1}{2}}}=1.$
符合题目要求.
符合题目要求.
答案
解析
备注