设锐角 $\triangle ABC$ 的三边长互不相等，$ O$ 为其外心，点 $A^\prime$ 在线段 $ AO $ 的延长线上，使得 $\angle B A^{\prime} A=\angle C A^{\prime} A$．过 $A^{\prime}$ 作 $A^{\prime} A_{1} \perp A C, A^{\prime} A_{2} \perp A B$，垂足分别为 $A_{1}, A_{2}$，作 $A H_{A} \perp B C$，垂足为 $H_{A}$．记 $\triangle H_{A} A_{1} A_{2}$ 的外接圆半径为 $R_A$，类似地可 $R_{B}, R_{C}$．求证：$\dfrac{1}{R_{A}}+\dfrac{1}{R_{B}}+\dfrac{1}{R_{C}}=\dfrac{2}{R}$
其中，$R$ 为 $ \triangle ABC$ 的外接圆半径．
其中，$R$ 为 $ \triangle ABC$ 的外接圆半径．
【难度】
【出处】
2008第23届CMO试题
【标注】
【答案】
略
【解析】
首先，易知 $A^\prime,B,O,C$ 四点共圆．事实上，如图所示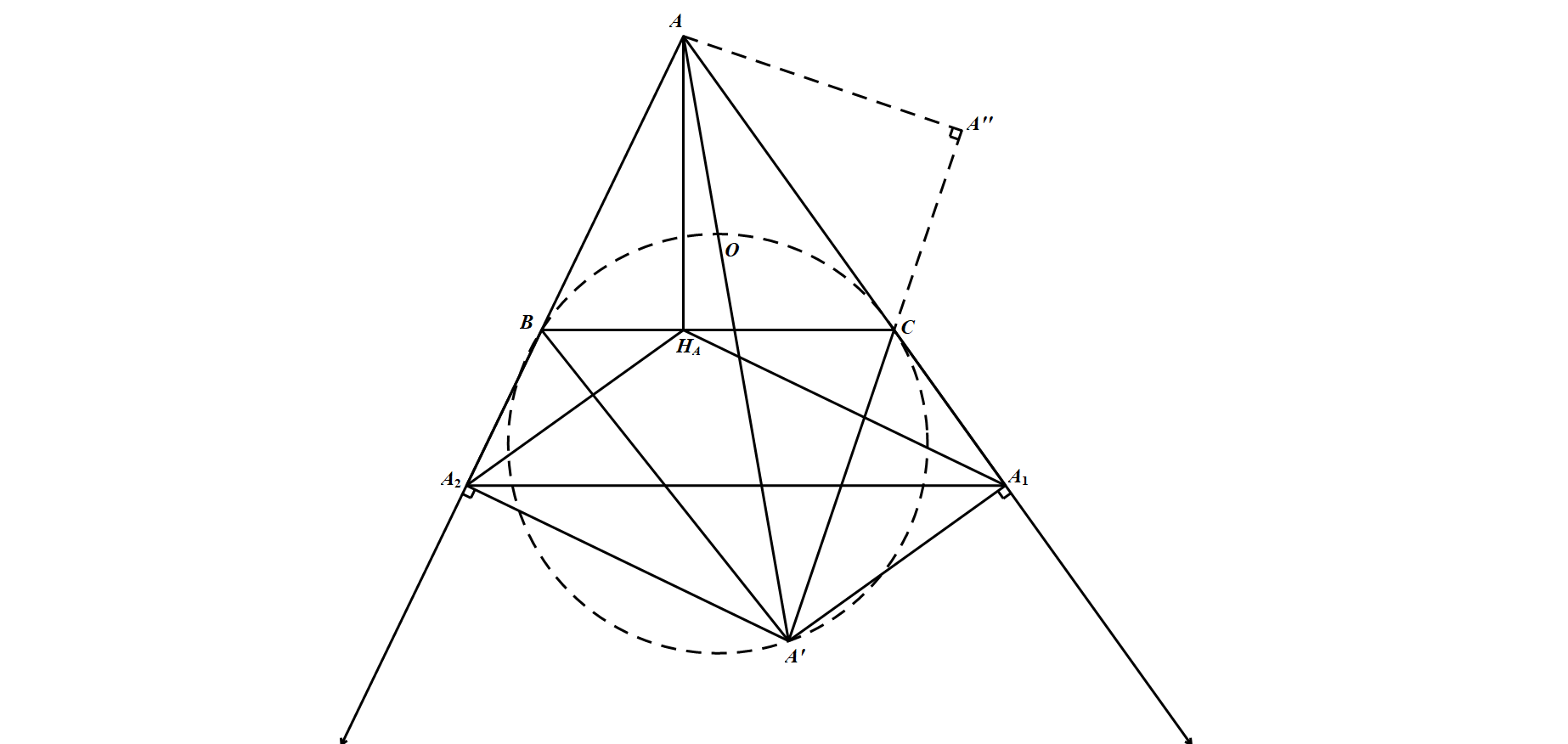
作 $\triangle BOC$ 的外接圆，设其与 $AO$ 交于点 $P$（不同于点 $A^\prime$）．则 $\angle B P A=\angle B C O=\angle C B O=\angle C P A$ 故 $\triangle P A^{\prime} C \cong \triangle P A^{\prime} B$，得 $A^{\prime} B=A^{\prime} C$，从而，$AB=AC$．矛盾．
其次 $\begin{aligned} \frac{A A_{2}}{A A^{\prime}} &=\cos \angle A_{2} A A^{\prime}=\sin C=\frac{H_{A} A}{A C} , \angle A_{2} A H_{A} =\dfrac{\pi}{2}-\angle B=\angle A^{\prime} A C \end{aligned}$ 以 $\triangle A_{2} A H_{A} \sim \triangle A^{\prime} A C$
同理 $\triangle A_{1} H_{A} A \sim \triangle A^{\prime} B A$
故 $\angle A_{2} H_{A} A=\angle A C A^{\prime},\angle A_{1} H_{A} A=\angle A B A^{\prime}$ 则 $\begin{aligned} \angle A_{1} H_{A} A_{2}=& 2 \pi-\angle A_{2} H_{A} A-\angle A_{1} H_{A} A= 2 \pi-\angle A C A^{\prime}-\angle A B A^{\prime}= \angle A+2\left(\frac{\pi}{2}-\angle A\right)=\pi-\angle A \end{aligned}$
以 $\dfrac{R}{R_{1}}=\dfrac{R}{\dfrac{A_{1} A_{2}}{2 \sin \angle A_{1} H_{A} A_{2}}}=\dfrac{2 R \sin A}{A_{1} A_{2}}=\dfrac{2 R \sin A}{A A^{\prime} \sin A}=\dfrac{2 R}{A A^{\prime}}$ 而 $\begin{aligned} A A^{\prime}= \dfrac{A A^{\prime \prime}}{\sin \angle A A^{\prime} C}=\dfrac{A H_{A}}{\sin \left(90^{\circ}-\angle A\right)}= \dfrac{A H_{A}}{\cos A}=\dfrac{2 S_{\triangle A B C}}{a \cos A} \end{aligned}$
其中，$A A^{\prime \prime} \perp A^{\prime} C$ 于点 $A^{\prime\prime}$．故 $\dfrac{1}{R_{A}}=\dfrac{a \cos A}{S_{\triangle A B C}}=\dfrac{\cos A}{R \sin B \sin C}=\dfrac{1}{R}(1-\cot B \cot C)$
同理 $\dfrac{1}{R_{B}}=\dfrac{1}{R}(1-\cot C \cot A),\dfrac{1}{R_{c}}=\dfrac{1}{R}(1-\cos A \cot B)$
注意到 $\cot A \cot B+\cot B \cot C+\cot C \cot A=1$ 所以 $\dfrac{1}{R_{A}}+\dfrac{1}{R_{B}}+\dfrac{1}{R_{C}}=\dfrac{2}{R}$
作 $\triangle BOC$ 的外接圆，设其与 $AO$ 交于点 $P$（不同于点 $A^\prime$）．则 $\angle B P A=\angle B C O=\angle C B O=\angle C P A$ 故 $\triangle P A^{\prime} C \cong \triangle P A^{\prime} B$，得 $A^{\prime} B=A^{\prime} C$，从而，$AB=AC$．矛盾．其次 $\begin{aligned} \frac{A A_{2}}{A A^{\prime}} &=\cos \angle A_{2} A A^{\prime}=\sin C=\frac{H_{A} A}{A C} , \angle A_{2} A H_{A} =\dfrac{\pi}{2}-\angle B=\angle A^{\prime} A C \end{aligned}$ 以 $\triangle A_{2} A H_{A} \sim \triangle A^{\prime} A C$
同理 $\triangle A_{1} H_{A} A \sim \triangle A^{\prime} B A$
故 $\angle A_{2} H_{A} A=\angle A C A^{\prime},\angle A_{1} H_{A} A=\angle A B A^{\prime}$ 则 $\begin{aligned} \angle A_{1} H_{A} A_{2}=& 2 \pi-\angle A_{2} H_{A} A-\angle A_{1} H_{A} A= 2 \pi-\angle A C A^{\prime}-\angle A B A^{\prime}= \angle A+2\left(\frac{\pi}{2}-\angle A\right)=\pi-\angle A \end{aligned}$
以 $\dfrac{R}{R_{1}}=\dfrac{R}{\dfrac{A_{1} A_{2}}{2 \sin \angle A_{1} H_{A} A_{2}}}=\dfrac{2 R \sin A}{A_{1} A_{2}}=\dfrac{2 R \sin A}{A A^{\prime} \sin A}=\dfrac{2 R}{A A^{\prime}}$ 而 $\begin{aligned} A A^{\prime}= \dfrac{A A^{\prime \prime}}{\sin \angle A A^{\prime} C}=\dfrac{A H_{A}}{\sin \left(90^{\circ}-\angle A\right)}= \dfrac{A H_{A}}{\cos A}=\dfrac{2 S_{\triangle A B C}}{a \cos A} \end{aligned}$
其中，$A A^{\prime \prime} \perp A^{\prime} C$ 于点 $A^{\prime\prime}$．故 $\dfrac{1}{R_{A}}=\dfrac{a \cos A}{S_{\triangle A B C}}=\dfrac{\cos A}{R \sin B \sin C}=\dfrac{1}{R}(1-\cot B \cot C)$
同理 $\dfrac{1}{R_{B}}=\dfrac{1}{R}(1-\cot C \cot A),\dfrac{1}{R_{c}}=\dfrac{1}{R}(1-\cos A \cot B)$
注意到 $\cot A \cot B+\cot B \cot C+\cot C \cot A=1$ 所以 $\dfrac{1}{R_{A}}+\dfrac{1}{R_{B}}+\dfrac{1}{R_{C}}=\dfrac{2}{R}$
答案
解析
备注
