设 $a \in(0,1), f(z)=z^{2}-z+a, z \in \mathbf{C}$ 证明：对任意满足 $ | z |\geqslant 1$ 的复数 $z$，存在满足 $|z_0|=1$ 的复数 $z_0$ 使得 $| f(z_0) |< f(z)$．
【难度】
【出处】
2015年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
首先我们证明如下引理：若复数 $z$ 在单位圆外，则存 在模为 $1$ 的复数 $z_0$ 对单位圆内的任意复数 $\omega$ 有 $\left|z_{0}-\omega\right|<|z-\omega|$．
引理的证明：如图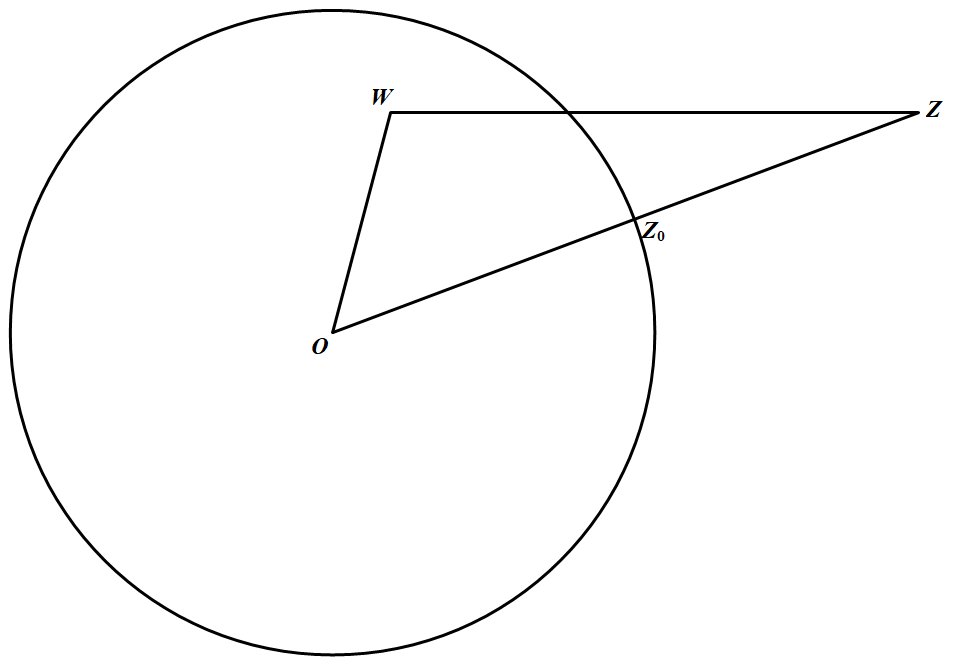
令 $z_0=\dfrac{z}{|z|}$，则 $Z_0$ 是 $Z$ 与圆心 $O$ 的连线段与圆的交点．注意到 $W$ 在圆的内部，则 $|\omega|<1=\left|z_{0}\right|$，故 $\angle O Z_{0} W<90^{\circ}, \angle W Z_{0} Z>90^{\circ}$．这里 $Z_0,W,Z$ 是以 $O$ 为原点的复平面上复数 $z_{0}, \omega, z$ 对应的点．
因此，$\left|z_{0}-\omega\right|<|z-\omega|$．
回到原题，我们先证明 $f(z)$ 的两根在单位圆内．
下面分两种情况：
（1）当 $0<a\leqslant\dfrac{1}{4}$ 时，因为 $\Delta=1-4 a \geqslant 0$，所以 $\boldsymbol{z}_{1}, \boldsymbol{z}_{2}$ 均为实数，于是由韦达定理知 $z_{1}, z_{2} \in(0,1)$．
（2）当 $\dfrac{1}{4} <a<1$ 时，因为 $\Delta=1-4 a<0$，所以 $z_1,z_2$ 互为共轭复数，于是由韦达定理 $\left|z_{1}\right|^{2}=\left|z_{2}\right|^{2}=z_{1} z_{2}=a \in(0,1)$．
由（1）、（2）可知 $f(z)$ 的两根 $z_1,z_2$ 均在单位圆内．
又 $\begin{aligned}|f(z)| &=\left|z^{2}-z+a\right| =\left|\left(z-z_{1}\right)\left(z-z_{2}\right)\right| =\left|z-z_{1}\right|\left|z-z_{2}\right| \end{aligned}$
当 $|z|=1$ 时，取 $z_{0}=z$，则 $|f(z)|=\left|f\left(z_{0}\right)\right|$；
当 $|z |> 1$ 时，由引理知存在 $z_0=\dfrac{z}{|z|}$ 有 $\left|z_{0}-z_{1}\right|<\left|z-z_{1}\right|,\left|z_{0}-z_{2}\right|<\left|z-z_{2}\right|$．于是 $\left|f\left(z_{0}\right)\right|<|f(z)|$．综上可知原题成立．
引理的证明：如图
令 $z_0=\dfrac{z}{|z|}$，则 $Z_0$ 是 $Z$ 与圆心 $O$ 的连线段与圆的交点．注意到 $W$ 在圆的内部，则 $|\omega|<1=\left|z_{0}\right|$，故 $\angle O Z_{0} W<90^{\circ}, \angle W Z_{0} Z>90^{\circ}$．这里 $Z_0,W,Z$ 是以 $O$ 为原点的复平面上复数 $z_{0}, \omega, z$ 对应的点．因此，$\left|z_{0}-\omega\right|<|z-\omega|$．
回到原题，我们先证明 $f(z)$ 的两根在单位圆内．
下面分两种情况：
（1）当 $0<a\leqslant\dfrac{1}{4}$ 时，因为 $\Delta=1-4 a \geqslant 0$，所以 $\boldsymbol{z}_{1}, \boldsymbol{z}_{2}$ 均为实数，于是由韦达定理知 $z_{1}, z_{2} \in(0,1)$．
（2）当 $\dfrac{1}{4} <a<1$ 时，因为 $\Delta=1-4 a<0$，所以 $z_1,z_2$ 互为共轭复数，于是由韦达定理 $\left|z_{1}\right|^{2}=\left|z_{2}\right|^{2}=z_{1} z_{2}=a \in(0,1)$．
由（1）、（2）可知 $f(z)$ 的两根 $z_1,z_2$ 均在单位圆内．
又 $\begin{aligned}|f(z)| &=\left|z^{2}-z+a\right| =\left|\left(z-z_{1}\right)\left(z-z_{2}\right)\right| =\left|z-z_{1}\right|\left|z-z_{2}\right| \end{aligned}$
当 $|z|=1$ 时，取 $z_{0}=z$，则 $|f(z)|=\left|f\left(z_{0}\right)\right|$；
当 $|z |> 1$ 时，由引理知存在 $z_0=\dfrac{z}{|z|}$ 有 $\left|z_{0}-z_{1}\right|<\left|z-z_{1}\right|,\left|z_{0}-z_{2}\right|<\left|z-z_{2}\right|$．于是 $\left|f\left(z_{0}\right)\right|<|f(z)|$．综上可知原题成立．
答案
解析
备注
