如图所示，三条直线 $l_1,l_2,l_3$ 两两平行，直线 $l_1$ 与 $l_2$ 的距离为 $p$，直线 $l_2$ 与 $l_3$ 的距离为 $\frac{p}{2}$．$A,B$ 是直线 $l_1$ 上的两个定点，且 $|AB|=2p$．$M,N$ 是直线 $l_2$ 上的两个动点，且 $|MN|=2p$．设 $\triangle AMN$ 的外心为 $C$，点 $C$ 到直线 $l_3$ 的距离为 $d$．试求 $d+|BC|$ 的最小值．
【难度】
【出处】
全国高中数学联赛模拟试题(1)
【标注】
【答案】
略
【解析】
如图所示，过点 $A$ 作 $AO\perp l_2$，垂足为 $O$，则 $AO$ 亦与 $l_1,l_3$ 垂直．以射线 $ON$ 为 $x$ 轴的非负半轴，射线 $OA$ 为 $y$ 轴的非负半轴建立平面直角坐标系 $xOy$．设 $M$ 的坐标为 $(a,0)$，$C$ 的坐标为 $(x,y)$，则 $N$ 的坐标为 $(a+2p,0)$．由 $C$ 在 $MN$ 的垂直平分线上，得 $x=\frac{a+(a+2p)}{2}$，即$$x-p=a.~~~~~ ① $$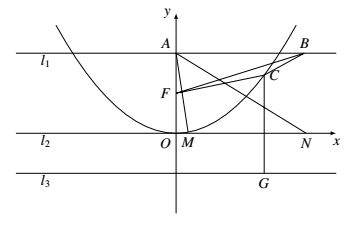
由 $|CM|=|CA|$，得 $x^2+(y-p)^2=(x-a)^2+y^2$，整理得$$2ax-2py+p^2-a^2=0.$$将式 ① 代入式 ②，整理得点 $C$ 的轨迹方程为 $x^2=2py$．它表示焦点为 $F(0,\frac{p}{2})$，准线为 $l_3:y=-\frac{p}{2}$ 的抛物线．过点 $C$ 作 $CG\perp l_3$，垂足为 $G$，则 $d=|CG|$．由抛物线的定义，知 $|CF|=|CG|$．从而$$d+|BC|=|CF|+|BC|\geqslant |BF|=\frac{\sqrt{17}}{2}p.$$其中等号当且仅当 $B,C,F$ 三点共线且 $C$ 在 $B,F$ 之间时成立，此时 $C$ 的坐标为 $\left(\frac{\sqrt{17}+1}{4}p,\frac{9+\sqrt{17}}{16}p\right)$．
因此，$d+|BC|$ 的最小值是 $\frac{\sqrt{17}}{2}p$．
由 $|CM|=|CA|$，得 $x^2+(y-p)^2=(x-a)^2+y^2$，整理得$$2ax-2py+p^2-a^2=0.$$将式 ① 代入式 ②，整理得点 $C$ 的轨迹方程为 $x^2=2py$．它表示焦点为 $F(0,\frac{p}{2})$，准线为 $l_3:y=-\frac{p}{2}$ 的抛物线．过点 $C$ 作 $CG\perp l_3$，垂足为 $G$，则 $d=|CG|$．由抛物线的定义，知 $|CF|=|CG|$．从而$$d+|BC|=|CF|+|BC|\geqslant |BF|=\frac{\sqrt{17}}{2}p.$$其中等号当且仅当 $B,C,F$ 三点共线且 $C$ 在 $B,F$ 之间时成立，此时 $C$ 的坐标为 $\left(\frac{\sqrt{17}+1}{4}p,\frac{9+\sqrt{17}}{16}p\right)$．因此，$d+|BC|$ 的最小值是 $\frac{\sqrt{17}}{2}p$．
答案
解析
备注
