如图所示，已知 $a>b>0, l_1,l_2$ 是双曲线 $\Gamma_1:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的两条渐近线，过椭圆 $\Gamma_2:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 的右焦点 $F$ 作直线 $m$，使得 $m\perp l_1$，直线 $m$ 与 $l_2$ 的交于点 $P$，与椭圆 $\Gamma_2$ 交于点 $A,B$．求 $\frac{|PB|}{|PA|}$ 的最大值以及此时椭圆 $\Gamma_2$ 的离心率．
【难度】
【出处】
全国高中数学联赛模拟试题(7)
【标注】
【答案】
略
【解析】
设 $c=\sqrt{a^2-b^2}$，则 $F$ 的坐标为 $(c,0)$，易知 $l_1:bx-ay=0,l_2:bx+ay=0, m: ax+by-ac=0$．联立 $m$ 与 $l_2$ 的方程，可解得 $P$ 的坐标为 $\left(\frac{a^2}{c},-\frac{ab}{c}\right)$，即点 $P$ 在椭圆 $\Gamma_2$ 的右准线上．
设 $\frac{|FA|}{|AP|}=\lambda$（$\lambda>0$），$A$ 的坐标为 $(x_A,y_A)$，则由定比分点公式可得$$X_A=\frac{c+\lambda\cdot \frac{a^2}{c}}{1+\lambda}, y_A=\frac{\lambda \cdot \left(-\frac{ab}{c}\right)}{1+\lambda}.$$将此坐标代入椭圆 $\Gamma_2$ 的方程，整理得$$(c^2+\lambda a^2)^2+\lambda^2a^4=a^2c^2(1+\lambda)^2\Rightarrow c^4+2\lambda^2a^4=a^2c^2+\lambda^2a^2c^2.$$上式两边同除以 $a^4$，并设 $e=\frac{c}{a}$（$0<e<1$），得$$e^4+2\lambda^2=e^2+\lambda^2e^2.$$从而$$\lambda^2=\frac{e^2-e^4}{2-e^2}=e^2+1-\frac{2}{2-e^2}=3-\left(2-e^2+\frac{2}{2-e^2}\right)\leqslant 3-2\sqrt{2}.$$当 $2-e^2=\sqrt{2}$，即 $e=\sqrt{2-\sqrt{2}}$ 时，上式等号成立，$\lambda$ 取到最大值 $\sqrt{2}-1$．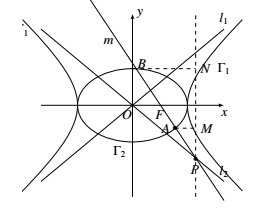
记 $t=\frac{|PB|}{|PA|}$．如图，作出椭圆 $\Gamma_2$ 的右准线 $n$．过点 $A, B$ 作 $n$ 的垂线，垂足分别为 $M,N$．由 $P$ 在这条准线上，知$$t=\frac{|PB|}{|PA|}=\frac{|NB|}{|MA|}=\frac{|FB|}{|FA|}\Rightarrow |BF|=t|AF|\Rightarrow |AB|=(1+t)|AF|.$$又 $|AB|=(t-1)|AP|$，故$$\lambda=\frac{|AF|}{|AP|}=\frac{t-1}{t+1}.$$从而$$\frac{t-1}{t+1}\leqslant \sqrt{2}-1\Rightarrow t\leqslant \sqrt{2}+1.$$因此，当椭圆 $\Gamma_2$ 的离心率 $e=\sqrt{2-\sqrt{2}}$ 时，$\frac{|PB|}{|PA|}$ 取得最大值 $\sqrt{2}+1$．
设 $\frac{|FA|}{|AP|}=\lambda$（$\lambda>0$），$A$ 的坐标为 $(x_A,y_A)$，则由定比分点公式可得$$X_A=\frac{c+\lambda\cdot \frac{a^2}{c}}{1+\lambda}, y_A=\frac{\lambda \cdot \left(-\frac{ab}{c}\right)}{1+\lambda}.$$将此坐标代入椭圆 $\Gamma_2$ 的方程，整理得$$(c^2+\lambda a^2)^2+\lambda^2a^4=a^2c^2(1+\lambda)^2\Rightarrow c^4+2\lambda^2a^4=a^2c^2+\lambda^2a^2c^2.$$上式两边同除以 $a^4$，并设 $e=\frac{c}{a}$（$0<e<1$），得$$e^4+2\lambda^2=e^2+\lambda^2e^2.$$从而$$\lambda^2=\frac{e^2-e^4}{2-e^2}=e^2+1-\frac{2}{2-e^2}=3-\left(2-e^2+\frac{2}{2-e^2}\right)\leqslant 3-2\sqrt{2}.$$当 $2-e^2=\sqrt{2}$，即 $e=\sqrt{2-\sqrt{2}}$ 时，上式等号成立，$\lambda$ 取到最大值 $\sqrt{2}-1$．
记 $t=\frac{|PB|}{|PA|}$．如图，作出椭圆 $\Gamma_2$ 的右准线 $n$．过点 $A, B$ 作 $n$ 的垂线，垂足分别为 $M,N$．由 $P$ 在这条准线上，知$$t=\frac{|PB|}{|PA|}=\frac{|NB|}{|MA|}=\frac{|FB|}{|FA|}\Rightarrow |BF|=t|AF|\Rightarrow |AB|=(1+t)|AF|.$$又 $|AB|=(t-1)|AP|$，故$$\lambda=\frac{|AF|}{|AP|}=\frac{t-1}{t+1}.$$从而$$\frac{t-1}{t+1}\leqslant \sqrt{2}-1\Rightarrow t\leqslant \sqrt{2}+1.$$因此，当椭圆 $\Gamma_2$ 的离心率 $e=\sqrt{2-\sqrt{2}}$ 时，$\frac{|PB|}{|PA|}$ 取得最大值 $\sqrt{2}+1$．
答案
解析
备注
