已知圆 $x^2+y^2=4$ 的切线与 $x$ 轴正半轴，$y$ 轴正半轴围成一个三角形．当该三角形的面积最小时切点为 $P$．双曲线 $C_1:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 过点 $P$ 且离心率为 $\sqrt 3$．
【难度】
【出处】
2014年高考辽宁卷（理）
【标注】
-
求 $C_1$ 的方程；标注答案$x^2-\dfrac {y^2}2=1$解析设圆 $x^2+y^2=4$ 的切线为 $x_0x+y_0y=4$，切点为 $(x_0,y_0)$ 满足$$x_0^2+y_0^2=4,x_0>0,y_0>0,$$则所围成的三角形面积为$$\dfrac 12\cdot \dfrac{4}{x_0}\cdot \dfrac{4}{y_0}=\dfrac{2\left(x_0^2+y_0^2\right)}{x_0y_0}=2\left(\dfrac{x_0}{y_0}+\dfrac{y_0}{x_0}\right),$$于是当 $x_0=y_0=\sqrt 2$ 时，该三角形的面积最小．结合双曲线 $C_1$ 过点 $P\left(\sqrt 2,\sqrt 2\right)$，离心率为 $\sqrt 3$，可得其方程为 $x^2-\dfrac{y^2}2=1$．
-
椭圆 $C_2$ 过点 $P$ 且与 $C_1$ 有相同的焦点，直线 $l$ 过 $C_2$ 的右焦点 $F$ 且与 $C_2$ 交于 $A,B$ 两点．若以线段 $AB$ 为直径的圆过点 $P$，求 $l$ 的方程．标注答案$x-\left(\dfrac{3\sqrt 6}2-1\right)y-\sqrt 3=0$ 或 $x+\left(\dfrac{\sqrt 6}2-1\right)y-\sqrt 3=0.$解析根据题意，椭圆 $C_2$ 的方程为 $C_2:\dfrac{x^2}6+\dfrac{y^2}3=1$．以 $AB$ 为直径的圆过 $P$，因此直线 $AB$ 过点 $P$ 或者线段 $AB$ 对 $P$ 点的张角为直角．
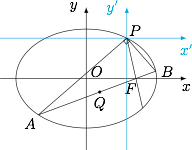以 $P$ 为原点，以原来的坐标轴方向为新的坐标轴方向重新建立平面直角坐标系 $x'Py'$，则新坐标系下的椭圆方程为$$\dfrac{(x'+\sqrt 2)^2}6+\dfrac{(y'+\sqrt 2)^2}3=1.$$整理得$$\dfrac 16x'^2+\dfrac 13y'^2+\dfrac{\sqrt 2}3x'+\dfrac{2\sqrt 2}3y'=0.$$设直线 $mx'+ny'=1$ 被椭圆截得的弦对 $P$ 的张角为直角，则化齐次联立，有$$\dfrac 16x'^2+\dfrac 13y'^2+\left(\dfrac{\sqrt 2}3x'+\dfrac{2\sqrt 2}3y'\right)\cdot (mx'+ny')=0.$$从而有$$\left(\dfrac 13+\dfrac{2\sqrt 2}3n\right)\cdot\left(\dfrac{y'}{x'}\right)^2+\left(\dfrac{\sqrt 2}3n+\dfrac{2\sqrt 2}3m\right)\cdot\left(\dfrac{y'}{x'}\right)+\dfrac 16+\dfrac{\sqrt 2}3m=0.$$根据题意，$PA\perp PB$，于是该方程的两根之积为 $-1$，即$$\dfrac{\dfrac 16+\dfrac{\sqrt 2}3m}{\dfrac 13+\dfrac{2\sqrt 2}3n}=-1,$$整理得$$-\dfrac{2\sqrt 2}3m-\dfrac{4\sqrt 2}3n=1,$$因此该直线恒过新坐标系的点 $Q\left(-\dfrac{2\sqrt 2}3,-\dfrac{4\sqrt 2}3\right)$，也即旧坐标系下的 $\left(\dfrac{\sqrt 2}3,-\dfrac{\sqrt 2}3\right)$．
此时可知直线 $QF$ 和直线 $PF$ 的方程为所求，结合 $F(\sqrt 3,0)$ 可得 $l$ 的方程为$$x-\left(\dfrac{3\sqrt 6}2-1\right)y-\sqrt 3=0$$或$$x+\left(\dfrac{\sqrt 6}2-1\right)y-\sqrt 3=0.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
