已知正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $1$，动点 $P$ 在正方体 $ABCD-A_1B_1C_1D_1$ 表面上运动，且 $PA=r$（$0<r<\sqrt 3$）．记点 $P$ 的轨迹的长度为 $f(r)$．
【难度】
【出处】
无
【标注】
-
求 $f\left(\dfrac 12\right)$；标注答案$\dfrac{3\pi}4$解析由于正方体绕其体对角线旋转 $120^\circ$ 后仍与自身重合，于是 $f(r)$ 为点 $P$ 在正方体的侧面 $ABB_1A_1$ 与 $BCC_1B_1$ 上的轨迹长度之和的 $3$ 倍．将右侧面 $BCC_1B_1$ 翻折至与侧面 $ABB_1A_1$ 重合，如图．稍加探索可以发现 $r=1$ 和 $r=\sqrt 2$ 是两个分界点．
当 $0<r\leqslant 1$ 时，有 $f(r)=\dfrac{3r\pi}2$，于是 $f\left(\dfrac 12\right)=\dfrac{3\pi}4$． -
求出关于 $r$ 的方程 $f(r)=k$ 的解的个数的所有可能的值，并说明理由．标注答案方程 $f(r)=k$ 的解的个数的所有可能值为 $0,2,3,4$解析当 $\sqrt 2\leqslant r<\sqrt 3$ 时，图中弧的半径为 $\sqrt{r^2-1}$，所对的圆心角为 $\dfrac{\pi}2-2\arccos\dfrac{1}{\sqrt{r^2-1}}$，记 $\theta=\arccos\dfrac{1}{\sqrt{r^2-1}}$，其中 $\theta\in\left[0,\dfrac{\pi}4\right)$，则对应的弧长$$l(\theta)=\left(\dfrac{\pi}2-2\theta\right)\cdot \dfrac{1}{\cos\theta},$$其导函数$$l'(\theta)=\dfrac{-2-2\theta\tan\theta+\dfrac{\pi}2\tan\theta}{\cos\theta}<0,$$于是随着 $r$ 的增大，$\theta$ 随之增大，对应的弧长随之减小，$f(r)$ 随之减小．
当 $1<r<\sqrt 2$ 时，设 $\theta=\arccos\dfrac{1}{r}$，其中 $\theta\in\left(0,\dfrac{\pi}4\right)$，则弧长之和$$h(\theta)=\left(\dfrac{\pi}2-2\theta\right)\cdot\dfrac{1}{\cos\theta}+\dfrac{\pi}2\cdot\tan\theta=\dfrac{\pi}2\cdot\dfrac{\sin\theta-\dfrac 4{\pi}\theta+1}{\cos\theta},$$于是$$h'(\theta)=\dfrac{\pi}2\cdot \dfrac{1+\sin\theta-\dfrac{4}{\pi}\left(\cos\theta+\theta\cdot\sin\theta\right)}{\cos^2\theta},$$设$$\varphi(\theta)=1+\sin\theta-\dfrac{4}{\pi}\left(\cos\theta+\theta\cdot\sin\theta\right),$$则 $\varphi(0)=1-\dfrac 4{\pi}<0$，$\varphi\left(\dfrac{\pi}4\right)=1-\dfrac{4}{\pi}\cdot \dfrac{\sqrt 2}2>0$，而$$\varphi'(\theta)=\cos\theta\cdot\left(1-\dfrac 4{\pi}\theta\right)>0,$$因此 $\varphi(\theta)$ 在 $\left(0,\dfrac{\pi}4\right)$ 上先负后正，对应的 $h(\theta)$ 在 $\left(0,\dfrac{\pi}4\right)$ 先递减再递增．
这样我们就可以勾勒出函数 $f(r)$ 的图象如下．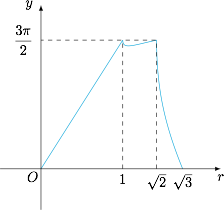
于是方程 $f(r)=k$ 的解的个数的所有可能值为 $0,2,3,4$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
