查看数据源：599165c52bfec200011e0b96
已知直线 $ l:x+ay-1=0\left(a\in {\mathbb{R}}\right) $ 是圆 $ C:x^2+y^2-4x-2y+1=0 $ 的对称轴．过点 $ A\left(-4,a\right) $ 作圆 $ C $ 的一条切线，切点为 $ B $，则 $ {\left|{AB}\right|}= $  \((\qquad)\)
A: $ 2 $
B: $ 4\sqrt 2 $
C: $ 6 $
D: $ 2\sqrt{10} $
【难度】
【出处】
2015年高考重庆卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    直线与圆
    >
    直线与圆的位置关系
  • 题型
    >
    解析几何
  • 知识点
    >
    解析几何
    >
    解析几何中的基本公式
    >
    两点间的距离公式
【答案】
C
【解析】
由题意可知，直线 $l$ 必过圆心，于是可求得 $a$ 值．然后在 $\mathrm {Rt}\triangle ABC$ 中应用勾股定理求得 $\left|AB\right|$ 长．由于直线 $ l:x+ay-1=0\left(a\in {\mathbb{R}}\right) $ 是圆 $ C:x^2+y^2-4x-2y+1=0 $ 的对称轴，所以直线 $l$ 经过圆心，求得圆心坐标为 $C\left(2,1\right)$，半径为 $2$，将圆心坐标代入直线 $l$ 的方程得 $a=-1$．所以 $A\left(-4,-1\right)$．由切线长求法可算得\[|AB|=\sqrt{|AC|^2-|CB|^2}=\sqrt{40-4}=6.\]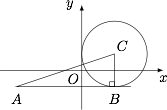
题目 答案 解析 备注
0.141739s