查看数据源：623467d7ea59ab000a73dbcb
如图，在四边形 $ABCD$ 中，$\angle D=2\angle B$，且 $AD=1, CD=3, \cos B=\dfrac{\sqrt{3}}{3}$．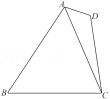
【难度】
【出处】
无
【标注】
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  1. 求 $AC$ 的长；
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      余弦定理
    答案
    （1）$AC=2\sqrt{3}$
    解析
    略
  2. 求四边形 $ABCD$ 面积的最大值．
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      余弦定理
    答案
    （2）四边形的面积最大值为 $ \dfrac{3\sqrt{6}+5\sqrt{2}}{2}$
    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.115666s