查看数据源：623468f5ea59ab000a73dbd5
如图，在正方形 $ABCD$ 中，点 $M, N$ 分别是边 $BC, CD$ 上的动点，且 $\angle MAN=45^\circ , \bigtriangleup CMN$ 的周长为 $2$，记 $t=\tan\angle MAB$．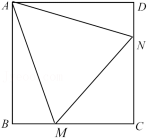
【难度】
【出处】
无
【标注】
  • 知识点
    >
    三角
    >
    解三角形
    >
    正弦定理
  • 知识点
    >
    三角
    >
    解三角形
    >
    余弦定理
  • 知识点
    >
    三角
    >
    解三角形
    >
    三角形面积公式
  1. 求正方形 $ABCD$ 的边长；
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      正弦定理
    答案
    $1$
    解析
    略
  2. 求 $\bigtriangleup AMN$ 面积的最小值．
    标注
    • 知识点
      >
      三角
      >
      解三角形
      >
      余弦定理
    • 知识点
      >
      三角
      >
      解三角形
      >
      三角形面积公式
    答案
    $ 2\sqrt{2}-2$
    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.115090s