“难度系数”反映试题的难易程度，难度系数越大，题目得分率越高，难度也就越小．“难度系数”的计算公式为 $L=1-\dfrac{Y}{W}$，其中 $L$ 为难度系数，$Y$ 为样本平均失分，$W$ 为试卷总分（一般为 $100$ 分或 $150$ 分）．某校高二年级的老师命制了某专题共 $5$ 套测试卷（总分 $150$ 分），用于对该校高二年级 $480$ 名学生进行每周测试，测试前根据自己对学生的了解，预估了每套试卷的难度系数，如表所示：
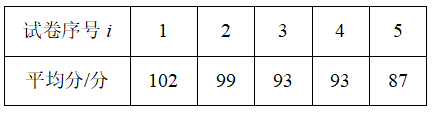
测试后，随机抽取了50名学生的数据进行统计，结果如下：
测试后，随机抽取了50名学生的数据进行统计，结果如下：【难度】
【出处】
无
【标注】
-
根据试卷 $2$ 的难度系数估计这 $480$ 名学生第 $2$ 套试卷的平均分；标注答案（1）平均分为 $96$ 分解析略
-
从抽取的 $50$ 名学生的 $5$ 套试卷中随机抽取 $2$ 套试卷，求抽取的 $2$ 套试卷中恰有 $1$ 套学生的平均分超过 $96$ 分的概率；标注答案（2）恰有一套学生的平均分超过96分的样本为 $(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)$，共 $6$ 种可能的结果，所以抽取的2套试卷中恰有 $1$ 套学生的平均分超过 $96$ 分的概率为 $ \dfrac{3}{5}$解析略
-
试卷的预估难度系数和实测难度系数之间会有偏差，设 $L'_i$ 为第 $i$ 套试卷的实测难度系数，并定义统计量 $S=\dfrac{1}{n} [(L_1′-L_1)^2+(L_2′-L_2)^2+\cdots+(L_n′-L_n)^2]$，若 $S<0.001$，则认为试卷的难度系数预估合理，否则认为不合理．以样本平均分估计总体平均分，试检验这 $5$ 套试卷难度系数的预估是否合理．标注答案（3）这5套试卷难度系数的预估合理解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
