查看数据源：623ad33bea59ab000a73dcf8
在箱子中有 $10$ 个小球，其中有 $3$ 个红球，$3$ 个白球，$4$ 个黑球．从这 $10$ 个球中任取 $3$ 个．求：
【难度】
【出处】
无
【标注】
  • 知识点
    >
    计数与概率
    >
    离散型随机变量
    >
    离散型随机变量的分布列
  • 知识点
    >
    计数与概率
    >
    离散型随机变量
    >
    离散型随机变量的分布列
  1. 取出的 $3$ 个球中红球的个数 $X$ 的分布列；
    标注
    • 知识点
      >
      计数与概率
      >
      离散型随机变量
      >
      离散型随机变量的分布列
    答案
    （1）$X$ 的分布列为：
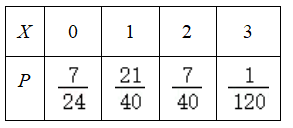    解析
    略
  2. 取出的 $3$ 个球中红球个数多于白球个数的概率．
    标注
    • 知识点
      >
      计数与概率
      >
      离散型随机变量
      >
      离散型随机变量的分布列
    答案
    （2）取出的3个球中红球个数多于白球个数的概率为 $ \dfrac{1}{3}$
    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.107810s