科研小组为提高某种水果的果径，设计了一套实验方案，并在两片果园中进行对比实验．其中实验园采用实验方案，对照园未采用．实验周期结束后，分别在两片果园中各随机选取 $100$ 个果实，按果径分成 $5$ 组进行统计：$[21, 26), [26, 31), [31, 36), [36, 41), [41, 46]$（单位，$mm$）．统计后分别制成如下的频率分布直方图，并规定果径达到 $36mm$ 及以上的为“大果”．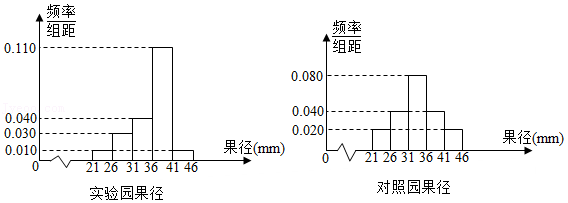
【难度】
【出处】
无
【标注】
-
请根据题中信息完成下面的列联表，并判断是否有 $99.9\%$ 的把握认为“大果”与“采用验方案”有关；
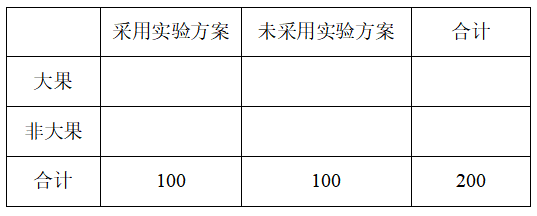标注答案（1）有 $99.9\%$ 的把握认为“大果”与“采用验方案”有关解析略 -
根据长期种植经验，可以认为对照园中的果径 $X$ 服从正态分布 $N(\mu, \sigma^2)$，其中 $ \mu$ 近似样本平均数 $ \overline{x}, \sigma \approx 5.5$．请估计对照园中果径落在区间 $(39, 50)$ 内的概率．（同一组中的数据以这组数据所在区间中点的值作代表）
标注答案（2）估计对照园中果径落在区间 $(39, 50)$ 内的概率为 $0.157$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
