某学校通过调查，了解了高三学生语文的学习情况．
【难度】
【出处】
无
【标注】
-
该校 $2000$ 名高三学生语文考试成绩 $X$ 服从正态分布，$X\sim N(110, 25)$，试估计这 $2000$ 名学生中大约有多少名同学语文考试成绩位于区间 $(100, 120]$ 之内？（人数按四舍五入取整）
附：$X\thicksim N(\mu, \sigma ^2)$，则 $P(\mu-\sigma\leqslant X\leqslant \mu+\sigma)\approx 0.6826, P(\mu-2\sigma\leqslant X\leqslant \mu+2\sigma)\approx 0.9544, P(\mu-3\sigma\leqslant X\leqslant \mu+3\sigma)\approx 0.9974$．标注答案（1）语文成绩在区间 $(100, 120]$ 内的人数为 $1909$（名）解析略 -
小明调查了自己班级同学对语文学习的爱好情况，在学生对高中语文学习的爱好情况统计中，有 $21$ 位男同学爱好学习高中语文，占所有男同学的 $ \dfrac{7}{10}$；有 $4$ 位女同学不爱好学习高中语文，占所有女同学的 $ \dfrac{1}{5}$．完成下列 $2\times 2$ 列联表，并根据列联表，回答是否有 $90\%$ 的把握认为学生是否爱好学习高中语文与学生性别有关．
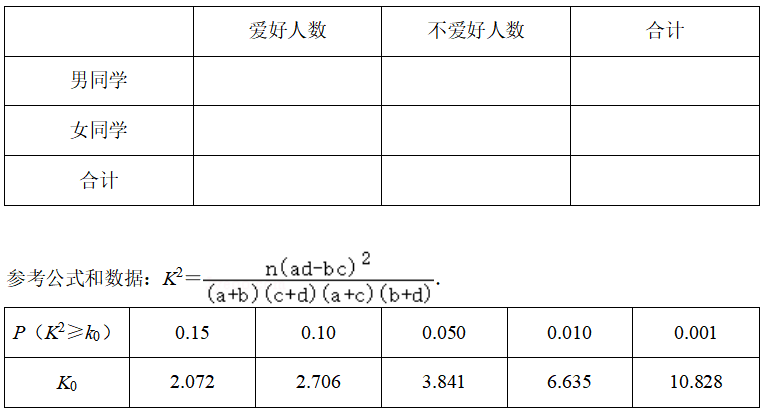标注答案（2）没有 $90\%$ 的把握认为学生是否爱好学习高中语文与学生性别有关解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
