查看数据源：623be537ea59ab0009118e45
设函数 $f(x)=\sin(\omega x+\varphi)$，$\left(\omega>0,-\dfrac{\pi}{2}<\varphi<0\right)$ 的最小正周期为 $\pi$，且 $f\left(\dfrac{\pi}{2}\right)=\dfrac{\sqrt{3}}{2}$．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的周期性
  • 知识点
    >
    三角
  1. 求 $\omega$ 和 $\varphi$ 的值；
    标注
    • 知识点
      >
      函数
      >
      函数的图象与性质
      >
      函数的周期性
    答案
    $2$；$-\dfrac {\pi}3$
    解析
    略
  2. 在给定的坐标系中作出函数 $f(x)$ 在 $[0,\pi]$ 上的图像．
    标注
    • 知识点
      >
      三角
    答案
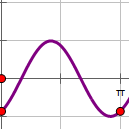    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.111277s