如图,四边形 $ABCD$ 中,已知 $\overrightarrow{AD}=2\overrightarrow{BC}$.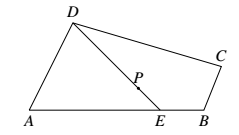

【难度】
【出处】
无
【标注】
-
(I)用 $\overrightarrow{AB}, \overrightarrow{AD}$ 表示 $\overrightarrow{DC}$;标注答案(I)$\because \overrightarrow{AD}=2\overrightarrow{BC}, \therefore \overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AD}$,则 $\overrightarrow{DC}=\overrightarrow{DA}+\overrightarrow{AB}+\overrightarrow{BC}=-\overrightarrow{AD}+\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}$解析略
-
(II)若 $\overrightarrow{AE}=2\overrightarrow{EB}, \overrightarrow{DP}=\lambda\overrightarrow{DE}$,当 $A, P, C$ 三点共线时,求实数 $\lambda$ 的值.标注答案(II)$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}, \overrightarrow{AP}=\overrightarrow{AD}+\overrightarrow{DP}, \because \overrightarrow{AE}=2\overrightarrow{EB}, \overrightarrow{DP}=\lambda\overrightarrow{DE}, \therefore \overrightarrow{AP}=\overrightarrow{AD}+\lambda\overrightarrow{DE}=\overrightarrow{AD}+\lambda(\overrightarrow{AE}-\overrightarrow{AD})=(1-\lambda)\overrightarrow{AD}+\lambda\overrightarrow{AE}=(1-\lambda)\overrightarrow{AD}+\dfrac{2}{3}\lambda\overrightarrow{AB}$,若 $A, P, C$ 三点共线时,则 $\dfrac{1-\lambda}{\dfrac{1}{2}}=\dfrac{\dfrac{2\lambda}{3}}{1}$,得 $1-\lambda=\dfrac{1}{2}\times\dfrac{2\lambda}{3}=\dfrac{\lambda}{3}$,得 $3-3\lambda=\lambda$,得 $\lambda=\dfrac{3}{4}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2