圆柱被一个平面截去一部分后与半球（半径为 $r$）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为 $16+20{\mathrm \pi} $，则 $r=$ \((\qquad)\) 
【难度】
【出处】
2015年高考全国Ⅰ卷（文）
【标注】
【答案】
B
【解析】
根据俯视图可以确定圆柱之上下底面与水平方向垂直，圆柱“躺”在水平面上．结合正视图当中的实线，推断出此几何体为圆柱被过上下底面圆心的平面所截的剩余部分与半球拼接而成．其表面积包含半球表面积、圆柱侧面积一半和圆柱截面矩形三个部分，列相应公式可解答问题．由正视图和俯视图可知，该几何体是一个半球与一个半圆柱构成的组合体，如图所示：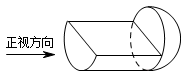
其中，球的半径为 $r$，圆柱的底面半径为 $r$，高为 $2r$，则所求表面积为\[\begin{split}S&\overset{\left[a\right]}=\dfrac 12\times 4{\mathrm \pi} r^2+{\mathrm \pi} r^2+4r^2+2{\mathrm \pi} r^2\\&=\left(5{\mathrm \pi} +4\right)r^2.\end{split}\]（推导中用到：$\left[a\right]$）
又因为 $S=16+20{\mathrm \pi} $，所以 $\left(5{\mathrm \pi} +4\right)r^2=16+20{\mathrm \pi} $，所以 $r=2$．
其中，球的半径为 $r$，圆柱的底面半径为 $r$，高为 $2r$，则所求表面积为\[\begin{split}S&\overset{\left[a\right]}=\dfrac 12\times 4{\mathrm \pi} r^2+{\mathrm \pi} r^2+4r^2+2{\mathrm \pi} r^2\\&=\left(5{\mathrm \pi} +4\right)r^2.\end{split}\]（推导中用到：$\left[a\right]$）又因为 $S=16+20{\mathrm \pi} $，所以 $\left(5{\mathrm \pi} +4\right)r^2=16+20{\mathrm \pi} $，所以 $r=2$．
题目
答案
解析
备注
