一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为 \((\qquad)\) 
【难度】
【出处】
2015年高考全国II卷（理）
【标注】
【答案】
D
【解析】
本题主要考查三视图的还原及体积的求法，难点在于“还原”，此时我们可以借助于长方体或正方体，利用三线交汇法还原三视图．由已知三视图知，该几何体为一个正方体截去了一个“大角”后剩余的部分（如图）．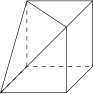
截去部分是一个三棱锥，其体积为\[V_1\overset{\left[a\right]}=\dfrac13\cdot\dfrac12\cdot1\cdot1\cdot1=\dfrac16;\]（其中用到 $\left[a\right]$）
剩余部分的体积为\[V_2=1^3-\dfrac16=\dfrac56.\]所以 $\dfrac{V_1}{V_2}=\dfrac15$．
截去部分是一个三棱锥，其体积为\[V_1\overset{\left[a\right]}=\dfrac13\cdot\dfrac12\cdot1\cdot1\cdot1=\dfrac16;\]（其中用到 $\left[a\right]$）剩余部分的体积为\[V_2=1^3-\dfrac16=\dfrac56.\]所以 $\dfrac{V_1}{V_2}=\dfrac15$．
题目
答案
解析
备注
