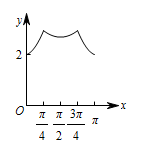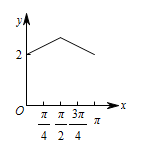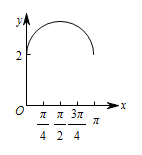如图,长方形 $ABCD$ 的边 $AB=2$,$BC=1$,$O$ 是 $AB$ 的中点,点 $P$ 沿着边 $BC$,$CD$ 与 $DA$ 运动,记 $\angle BOP=x$.将动点 $P$ 到 $A$,$B$ 两点距离之和表示为 $x$ 的函数 $f\left(x\right)$,则 $y=f\left(x\right)$ 的图象大致为 \((\qquad)\) 

【难度】
【出处】
2015年高考全国II卷(理)
【标注】
【答案】
B
【解析】
本题可以先逐段求出解析式,再判断图象,但计算量较大,对于选择、填空题来说,我们可以分析关键点处的函数值,或特定区间上的函数值变化趋势来排除错误选项.用排除法排除错误选项.
当 $x\in\left[0,\dfrac{\mathrm \pi} {4}\right]$ 时,$y=PA+PB=\sqrt {4+\tan^2x}+\tan x$,图象不会是直线段,从而排除A,C;
当 $x\in\left[\dfrac{\mathrm \pi} {4},\dfrac{3{\mathrm \pi} } {4}\right]$ 时,$f\left(\dfrac{\mathrm \pi} {4}\right)=f\left(\dfrac{3{\mathrm \pi} } {4}\right)=1+\sqrt5$,$f\left(\dfrac{\mathrm \pi} {2}\right)=2\sqrt2$.
因为 $2\sqrt2<1+\sqrt5$,所以 $f\left(\dfrac{\mathrm \pi} {2}\right)<f\left(\dfrac{\mathrm \pi} {4}\right)=f\left(\dfrac{3{\mathrm \pi} } {4}\right)$,从而排除D,故选B.
当 $x\in\left[0,\dfrac{\mathrm \pi} {4}\right]$ 时,$y=PA+PB=\sqrt {4+\tan^2x}+\tan x$,图象不会是直线段,从而排除A,C;
当 $x\in\left[\dfrac{\mathrm \pi} {4},\dfrac{3{\mathrm \pi} } {4}\right]$ 时,$f\left(\dfrac{\mathrm \pi} {4}\right)=f\left(\dfrac{3{\mathrm \pi} } {4}\right)=1+\sqrt5$,$f\left(\dfrac{\mathrm \pi} {2}\right)=2\sqrt2$.
因为 $2\sqrt2<1+\sqrt5$,所以 $f\left(\dfrac{\mathrm \pi} {2}\right)<f\left(\dfrac{\mathrm \pi} {4}\right)=f\left(\dfrac{3{\mathrm \pi} } {4}\right)$,从而排除D,故选B.
题目
答案
解析
备注