已知 $A$，$B$ 为双曲线 $E$ 的左、右顶点，点 $M$ 在 $E$ 上，$\triangle ABM$ 为等腰三角形，且顶角为 $120^\circ$，则 $E$ 的离心率为 \((\qquad)\)
【难度】
【出处】
2015年高考全国II卷（理）
【标注】
【答案】
D
【解析】
解本题有两个关键点：一是“以静制动”假设点 $M$ 的位置，画出草图；二是表示出点 $M$ 的坐标．设双曲线方程为 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\left(a>0,b>0\right)$．不妨取点 $M$ 在第一象限，如图．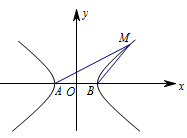
则 $\angle ABM=120^\circ$，且 $|BM|=|AB|=2a$，
所以点 $M$ 的坐标为\[\left(2a,\sqrt 3a\right).\]因为点 $M$ 在双曲线上，所以\[\dfrac{4a^2}{a^2}-\dfrac{3a^2}{b^2}=1,\]又 $c^2=a^2+b^2$，所以 $e=\dfrac{c}{a}=\sqrt 2$．
则 $\angle ABM=120^\circ$，且 $|BM|=|AB|=2a$，所以点 $M$ 的坐标为\[\left(2a,\sqrt 3a\right).\]因为点 $M$ 在双曲线上，所以\[\dfrac{4a^2}{a^2}-\dfrac{3a^2}{b^2}=1,\]又 $c^2=a^2+b^2$，所以 $e=\dfrac{c}{a}=\sqrt 2$．
题目
答案
解析
备注
