在 $\triangle ABC$ 中，$\angle BAC=90^\circ$，以 $AB$ 为一边向 $\triangle ABC$ 外作等边三角形 $ABD$，$\angle BCD=2\angle ACD$，$\overrightarrow {AD}=\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}$，则 $\lambda+\mu=$ ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {1-\sqrt 3}2$
【解析】
如图建系，设 $A(0,0)$，$B(0,2)$，$C(-m,0)$（$m>0$），$D(\sqrt 3,1)$，$\angle DCA=\theta$，则 $\angle BCA=3\theta$．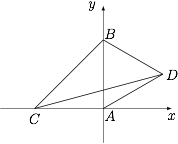
根据三倍角公式，有\[\tan3\theta=\dfrac{3\tan\theta-\tan^3\theta}{1-3\tan^2\theta},\]于是\[\dfrac 2m=\dfrac{3\cdot \dfrac{1}{\sqrt 3+m}-\left(\dfrac{1}{\sqrt 3+m}\right)^3}{1-3\cdot \left(\dfrac{1}{\sqrt 3+m}\right)^2},\]也即\[\dfrac 2m=\dfrac{8+6\sqrt 3m+3m^2}{m\left(6+3\sqrt 3m+m^2\right)},\]解得 $m=2$，于是\[\lambda=\dfrac 12,\mu=-\dfrac{\sqrt 3}2,\]从而\[\lambda+\mu=\dfrac{1-\sqrt 3}2.\]
根据三倍角公式，有\[\tan3\theta=\dfrac{3\tan\theta-\tan^3\theta}{1-3\tan^2\theta},\]于是\[\dfrac 2m=\dfrac{3\cdot \dfrac{1}{\sqrt 3+m}-\left(\dfrac{1}{\sqrt 3+m}\right)^3}{1-3\cdot \left(\dfrac{1}{\sqrt 3+m}\right)^2},\]也即\[\dfrac 2m=\dfrac{8+6\sqrt 3m+3m^2}{m\left(6+3\sqrt 3m+m^2\right)},\]解得 $m=2$，于是\[\lambda=\dfrac 12,\mu=-\dfrac{\sqrt 3}2,\]从而\[\lambda+\mu=\dfrac{1-\sqrt 3}2.\]
题目
答案
解析
备注
