某三棱锥的三视图如图所示，则该三棱锥的表面积是 \((\qquad)\) 
【难度】
【出处】
2015年高考北京卷（理）
【标注】
【答案】
C
【解析】
首先结合三视图还原这个三棱锥，得到其直观图，分别计算各个表面的面积．由可得该三棱锥的直观图为：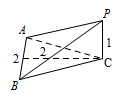
其中，$PC\perp 平面 ABC$，$PC=1$，底面 $ABC$ 为等腰三角形，底边 $AB=2$ 且 $AB$ 边上的高为 $2$．
$ S_{\triangle{PBC}}=S_{\triangle{PAC}}=\dfrac 12 \cdot 1\cdot \sqrt 5=\dfrac{\sqrt 5}{2} $，$S_{\triangle{ABC}}=\dfrac 12\cdot 2\cdot 2=2$，$S_{\triangle{PAB}}=\dfrac 12\cdot 2\cdot \sqrt 5=\sqrt 5$，故所求表面积为 $2+2\sqrt 5$．
其中，$PC\perp 平面 ABC$，$PC=1$，底面 $ABC$ 为等腰三角形，底边 $AB=2$ 且 $AB$ 边上的高为 $2$．$ S_{\triangle{PBC}}=S_{\triangle{PAC}}=\dfrac 12 \cdot 1\cdot \sqrt 5=\dfrac{\sqrt 5}{2} $，$S_{\triangle{ABC}}=\dfrac 12\cdot 2\cdot 2=2$，$S_{\triangle{PAB}}=\dfrac 12\cdot 2\cdot \sqrt 5=\sqrt 5$，故所求表面积为 $2+2\sqrt 5$．
题目
答案
解析
备注
