如图，函数 $f\left(x\right)$ 的图象为折线 $ACB$，则不等式 $f\left(x\right)\geqslant{\log _2}\left(x+1\right)$ 的解集是 \((\qquad)\) 
【难度】
【出处】
2015年高考北京卷（理）
【标注】
【答案】
C
【解析】
利用函数图象解决函数不等式．在同一坐标系下，画出各自图象，找到 $f(x)$ 在 $\log_2(x+1)$ 上方的部分对应的 $x$ 的取值即可．令 $ g\left(x\right)=\log_2\left(x+1\right) $，定义域为 $\left(-1,+\infty\right)$．作出函数 $g\left(x\right)$ 的图象，如图所示：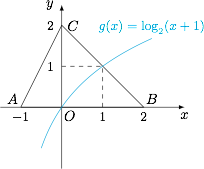
根据 $B,C$ 坐标可求得直线 $BC$ 的方程为 $x+y-2=0$，由\[\begin{cases}x+y-2=0,\\y=\log _2\left(x+1\right),\end{cases}\]得\[\begin{cases}x=1,\\y=1.\end{cases}\]结合图象可知：当 $-1<x<1$ 时，$f\left(x\right)>g\left(x\right)$；当 $x=1$ 时，$f\left(x\right)=g\left(x\right)$．
故不等式 $f\left(x\right)\geqslant\log _2\left(x+1\right)$ 的解集是 $\left\{x \left|\right. -1<x\leqslant1\right\}$．
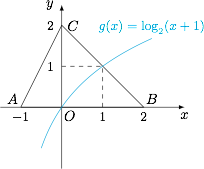根据 $B,C$ 坐标可求得直线 $BC$ 的方程为 $x+y-2=0$，由\[\begin{cases}x+y-2=0,\\y=\log _2\left(x+1\right),\end{cases}\]得\[\begin{cases}x=1,\\y=1.\end{cases}\]结合图象可知：当 $-1<x<1$ 时，$f\left(x\right)>g\left(x\right)$；当 $x=1$ 时，$f\left(x\right)=g\left(x\right)$．故不等式 $f\left(x\right)\geqslant\log _2\left(x+1\right)$ 的解集是 $\left\{x \left|\right. -1<x\leqslant1\right\}$．
题目
答案
解析
备注
