已知函数 $f(x)=x(1+a|x|)$，设关于 $x$ 的不等式 $f(x+a)<f(x)$ 的解集为 $M$，若 $\left[-\dfrac 12,\dfrac 12\right]\subseteq M$，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac{1-\sqrt 5}{2},0\right)$
【解析】
首先我们能得到 $f(x)$ 为奇函数，单调区间的情况与 $a$ 的正负有关，且 $a\ne 0$．
当 $a>0$ 时，$f(x)$ 在 $\mathbb{R}$ 上单调递增，不等式不可能成立．
所以 $a<0$，此时 $f(x)$ 的草图如下（可以先画出 $[0,+\infty)$ 的部分再对称过来）
此函数在整个定义域上没有单调性，无法直接将函数不等式转化成与自变量相关的不等式，我们需要从函数的图象出发，看看函数不等式 $f(x+a)<f(x)$ 有什么直观意义：
取 $A(x,f(x))$，$B(x+a,f(x+a))$，当 $A$ 点与 $B$ 点在函数图象上变动时，点 $B$ 在点 $A$ 的下方时对应的 $A$ 点的横坐标满足函数不等式，如图：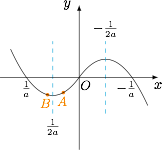
因为 $x=0$ 时，不等式成立，所以我们有$$f(a)<0,$$故 $a>\dfrac 1a$，解得 $-1<a<0$．
从而 $-\dfrac{1}{2a}>\dfrac 12$，结合图象知要满足 $\left[-\dfrac 12,\dfrac 12\right]\subseteq M$，只需考虑 $x=-\dfrac 12$ 的情况即可，当$$\dfrac{-\dfrac 12-\dfrac 12+a}{2}>\dfrac{1}{2a}$$时，有$$f\left(-\dfrac 12+a\right)<f\left(-\dfrac 12\right),$$解得 $a>\dfrac{1-\sqrt 5}{2}$．
当 $a>0$ 时，$f(x)$ 在 $\mathbb{R}$ 上单调递增，不等式不可能成立．
所以 $a<0$，此时 $f(x)$ 的草图如下（可以先画出 $[0,+\infty)$ 的部分再对称过来）
此函数在整个定义域上没有单调性，无法直接将函数不等式转化成与自变量相关的不等式，我们需要从函数的图象出发，看看函数不等式 $f(x+a)<f(x)$ 有什么直观意义：取 $A(x,f(x))$，$B(x+a,f(x+a))$，当 $A$ 点与 $B$ 点在函数图象上变动时，点 $B$ 在点 $A$ 的下方时对应的 $A$ 点的横坐标满足函数不等式，如图：
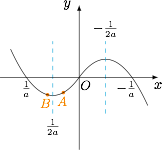因为 $x=0$ 时，不等式成立，所以我们有$$f(a)<0,$$故 $a>\dfrac 1a$，解得 $-1<a<0$．从而 $-\dfrac{1}{2a}>\dfrac 12$，结合图象知要满足 $\left[-\dfrac 12,\dfrac 12\right]\subseteq M$，只需考虑 $x=-\dfrac 12$ 的情况即可，当$$\dfrac{-\dfrac 12-\dfrac 12+a}{2}>\dfrac{1}{2a}$$时，有$$f\left(-\dfrac 12+a\right)<f\left(-\dfrac 12\right),$$解得 $a>\dfrac{1-\sqrt 5}{2}$．
题目
答案
解析
备注
