母线长为 $2\sqrt 3$，底面半径为 $\sqrt 3$ 的圆锥内有一球 $O$ 与圆锥的侧面、底面都相切，现放入一些小球，小球与圆锥底面、侧面、球 $O$ 都相切，这样的小球最多可放入 个．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图．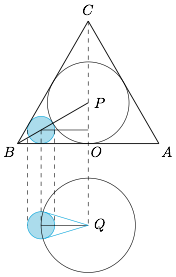
对圆锥的轴截面 $ABC$（这是一个边长为 $2\sqrt 3$ 的正三角形）进行分析，可得放入的小球的半径\[r=\dfrac 16BP=\dfrac 13.\]考虑小球在底面上的投影，过 $Q$ 作小球在底面上投影圆的切线，可得该圆在 $Q$ 处的张角\[\theta=2\arcsin\dfrac{r}{\dfrac 23BO}=2\arcsin\dfrac{\sqrt 3}6,\]由于\[\sin\dfrac{\pi}{10}=\dfrac{\sqrt 5-1}4>\dfrac{\sqrt 3}6,\]于是\[\dfrac{\theta}2<\dfrac{\pi}{10},\]又\[\sin\dfrac{\pi}{11}<\dfrac{\pi}{11}<\dfrac{\sqrt 3}6,\]于是\[\dfrac{\theta}2>\dfrac{\pi}{11},\]从而\[10<\dfrac{2\pi}{\theta}<11,\]因此这样的小球最多可以放入 $10$ 个．
对圆锥的轴截面 $ABC$（这是一个边长为 $2\sqrt 3$ 的正三角形）进行分析，可得放入的小球的半径\[r=\dfrac 16BP=\dfrac 13.\]考虑小球在底面上的投影，过 $Q$ 作小球在底面上投影圆的切线，可得该圆在 $Q$ 处的张角\[\theta=2\arcsin\dfrac{r}{\dfrac 23BO}=2\arcsin\dfrac{\sqrt 3}6,\]由于\[\sin\dfrac{\pi}{10}=\dfrac{\sqrt 5-1}4>\dfrac{\sqrt 3}6,\]于是\[\dfrac{\theta}2<\dfrac{\pi}{10},\]又\[\sin\dfrac{\pi}{11}<\dfrac{\pi}{11}<\dfrac{\sqrt 3}6,\]于是\[\dfrac{\theta}2>\dfrac{\pi}{11},\]从而\[10<\dfrac{2\pi}{\theta}<11,\]因此这样的小球最多可以放入 $10$ 个．
题目
答案
解析
备注
