若变量 $x,y$ 满足约束条件 $\begin{cases} y\leqslant x,\\ x+y\leqslant 4,\\ y\geqslant k,\end{cases}$ 且 $z=2x+y$ 的最小值为 $-4$，则 $k=$ ．
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（二测）
【标注】
【答案】
$-\dfrac 43$
【解析】
如图．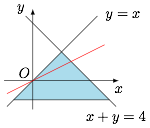
根据题意，当 $(x,y)=(k,k)$（$k\leqslant 2$）时 $z$ 取得最小值，因此\[2\cdot k+k=-4,\]解得 $k=-\dfrac 43$．
根据题意，当 $(x,y)=(k,k)$（$k\leqslant 2$）时 $z$ 取得最小值，因此\[2\cdot k+k=-4,\]解得 $k=-\dfrac 43$．
题目
答案
解析
备注
