如图，正方形 $ABCD$ 的边长为 $6$，点 $E,F$ 分别在边 $AD,BC$ 上，且 $DE=2EA$，$CF=2FB$，如果对于常数 $\lambda$，在正方形 $ABCD$ 的四条边上，有且只有 $6$ 个不同的点 $P$，使得 $\overrightarrow {PE}\cdot\overrightarrow {PF}=\lambda$ 成立，那么 $\lambda$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(0,4)$
【解析】
记 $\overrightarrow {PE}\cdot\overrightarrow{PF}=\lambda$，当 $P$ 点在正方形的边上连续运动时，$\lambda$ 连续变化，所以如果对变化中几个特别的点：端点与极值点求出具体的值来，就可以通过这些值确定各条线段上 $\lambda$ 的取值范围．
例如，当点 $P$ 从 $E$ 运动到 $D$ 时，$\lambda$ 的值从 $0$ 连续增长到 $16$；类似地可以得出，当点 $P$ 在 $EA$、$FB$、$FC$ 上运动时 $\lambda$ 的变化都是从小到大的；
当点 $P$ 从 $D$ 点运动到 $C$ 点时，这个值先减小再增大，当点 $P$ 在 $CD$ 的中点处时，$\lambda$ 取到极小值 $7$，同理当点 $P$ 在 $AB$ 的中点处时，$\lambda$ 也取到极小值 $-5$；将这些端点与极值点处的值标在正方形上，如下图：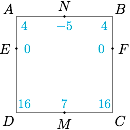
以从 $E$ 点出发逆时针旋转移动的距离为横坐标，$\lambda$ 为纵坐标可以作出对应的函数草图（单调性和极值吻合），如图．可知 $\lambda$ 的取值范围是 $(0,4$）．
例如，当点 $P$ 从 $E$ 运动到 $D$ 时，$\lambda$ 的值从 $0$ 连续增长到 $16$；类似地可以得出，当点 $P$ 在 $EA$、$FB$、$FC$ 上运动时 $\lambda$ 的变化都是从小到大的；
当点 $P$ 从 $D$ 点运动到 $C$ 点时，这个值先减小再增大，当点 $P$ 在 $CD$ 的中点处时，$\lambda$ 取到极小值 $7$，同理当点 $P$ 在 $AB$ 的中点处时，$\lambda$ 也取到极小值 $-5$；将这些端点与极值点处的值标在正方形上，如下图：
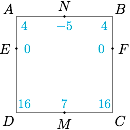以从 $E$ 点出发逆时针旋转移动的距离为横坐标，$\lambda$ 为纵坐标可以作出对应的函数草图（单调性和极值吻合），如图．可知 $\lambda$ 的取值范围是 $(0,4$）．
题目
答案
解析
备注
