已知关于 $x$ 的方程 $a\sin x+b\cos x+c=0$ 在 $[0,2{\mathrm \pi})$ 内有两个不同的实数解 $\alpha,\beta$，其中 $a,b,c$ 均为非零常数，则 $\sin(\alpha+\beta)=$ ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{2ab}{a^2+b^2}$
【解析】
设 $P(\cos x,\sin x)$ 是单位圆上一点，$Q(b,a)$，则根据题意，有 $\overrightarrow{OP}\cdot \overrightarrow{OQ}=-c$，因此 $A(\cos\alpha,\sin\alpha)$ 与 $B(\cos\beta,\sin\beta)$ 的连线 $AB$ 与直线 $OQ$ 垂直，如图．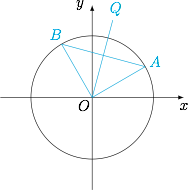
由垂径定理可得角 $\dfrac{\alpha+\beta}2$ 的终边为 $OQ$，因此$$\sin(\alpha+\beta)=2\sin\dfrac{\alpha+\beta}2\cos\dfrac{\alpha+\beta}2=2\cdot \dfrac{a}{\sqrt{a^2+b^2}}\cdot \dfrac{b}{\sqrt{a^2+b^2}}=\dfrac{2ab}{a^2+b^2}.$$
由垂径定理可得角 $\dfrac{\alpha+\beta}2$ 的终边为 $OQ$，因此$$\sin(\alpha+\beta)=2\sin\dfrac{\alpha+\beta}2\cos\dfrac{\alpha+\beta}2=2\cdot \dfrac{a}{\sqrt{a^2+b^2}}\cdot \dfrac{b}{\sqrt{a^2+b^2}}=\dfrac{2ab}{a^2+b^2}.$$
题目
答案
解析
备注
