设 $f(x)$ 是定义在 $\mathbb{R}$ 上的奇函数，且当 $x\geqslant 0$ 时，$f(x)=x^2$，若对于任意的 $x\in [t,t+2]$，不等式 $f(x+t)\geqslant 2f(x)$ 恒成立，则实数 $t$ 的取值范围是 ．
【难度】
【出处】
2012年全国高中数学联赛（一试）
【标注】
【答案】
$[\sqrt{2},+\infty)$
【解析】
我们见过类似的问题，比如：函数 $g(x)$ 是奇函数，且在 $\mathbb{R}$ 上单调递减，解不等式 $g(x)+g(x^2)<0$．此不等式等价于$$g(x)<-g(x^2)=g(-x^2),$$于是函数不等式转化成与自变量相关的不等式$$x>-x^2,$$从而得到结果．在本题中函数不等式中的负号变成了系数 $2$．
根据题意，有$$f(x)=\begin{cases}x^2,&x\geqslant 0,\\-x^2,&x<0.\end{cases}$$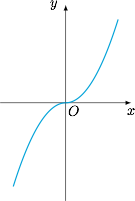
如图，$f(x)$ 具有很好的单调性——在 $\mathbb{R}$ 上单调递增．
如果能将系数 $2$ 转移到自变量中，则可以和上面的题一样，根据单调性将函数不等式变成普通的不等式．
有了这个方向，不难得到 $2f(x)=f(\sqrt 2x)$，所以$$\forall x\in [t ,t+2],f(x+t)\geqslant f(\sqrt 2 x),$$即$$\forall x\in [t ,t+2],x+t\geqslant \sqrt{2} x,$$从而有$$\left(\sqrt 2-1\right)(t+2)\leqslant t,$$解得 $t\geqslant \sqrt 2$．
根据题意，有$$f(x)=\begin{cases}x^2,&x\geqslant 0,\\-x^2,&x<0.\end{cases}$$
如图，$f(x)$ 具有很好的单调性——在 $\mathbb{R}$ 上单调递增．如果能将系数 $2$ 转移到自变量中，则可以和上面的题一样，根据单调性将函数不等式变成普通的不等式．
有了这个方向，不难得到 $2f(x)=f(\sqrt 2x)$，所以$$\forall x\in [t ,t+2],f(x+t)\geqslant f(\sqrt 2 x),$$即$$\forall x\in [t ,t+2],x+t\geqslant \sqrt{2} x,$$从而有$$\left(\sqrt 2-1\right)(t+2)\leqslant t,$$解得 $t\geqslant \sqrt 2$．
题目
答案
解析
备注
