查看数据源：5a542702cf5696000778cffa
若平面向量 $\overrightarrow a,\overrightarrow b$ 满足 $\overrightarrow a\cdot \overrightarrow a=1$，$\overrightarrow b\cdot \overrightarrow b=4$，$\overrightarrow a\cdot \overrightarrow b=1$，$\overrightarrow e$ 是平面内的单位向量，则 $\Big|\overrightarrow a\cdot \overrightarrow e\Big|+\Big|\overrightarrow b\cdot \overrightarrow e\Big|$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    向量
    >
    向量的运算
    >
    向量的数量积
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
【答案】
$\left[\dfrac{\sqrt 3}2,\sqrt 7\right]$
【解析】
记 $\overrightarrow {OA}=\overrightarrow {a},\overrightarrow {OB}=\overrightarrow {b}$，$\overrightarrow {OE}=\overrightarrow {e}$，则题意知$$OA=1,OB=2,\angle AOB=\dfrac {\pi}{3}.$$且点 $E$ 在以 $O$ 为圆心的单位圆上，如图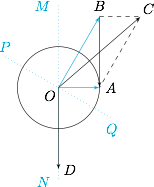：容易计算得到$$\Big|\overrightarrow {OC}\Big|=\Big|\overrightarrow {a}+\overrightarrow {b}\Big|=\sqrt 7,\Big|\overrightarrow {OD}\Big|=\Big|\overrightarrow {a}-\overrightarrow {b}\Big|=\sqrt 3.$$过点 $O$ 作 $MN\perp OA,PQ\perp OB$，于是平面区域划分成四个部分$$QOM,MOP,PON,NOQ,$$类似于四个象限，其中当点 $E$ 在“第一、三象限（$QOM$ 与 $PON$）”内（含边界）时，$\overrightarrow {a}\cdot\overrightarrow {e}$ 与 $\overrightarrow {b}\cdot\overrightarrow {e}$ 同号（或其中一个为零），此时有$$\Big|\overrightarrow a\cdot \overrightarrow e\Big|+\Big|\overrightarrow b\cdot \overrightarrow e\Big|=\Big|(\overrightarrow {a}+\overrightarrow {b})\cdot\overrightarrow {e}\Big|=\overrightarrow {OC}\cdot \overrightarrow {OE}\in\left[\dfrac {\sqrt 3}2,\sqrt 7\right].$$当点 $E$ 在“第二、四象限（$MOP$ 与 $NOQ$）”内（含边界）时，$\overrightarrow {a}\cdot\overrightarrow {e}$ 与 $\overrightarrow {b}\cdot\overrightarrow {e}$ 异号（或其中一个为零），此时有$$\Big|\overrightarrow a\cdot \overrightarrow e\Big|+\Big|\overrightarrow b\cdot \overrightarrow e\Big|=\Big|(\overrightarrow {a}-\overrightarrow {b})\cdot\overrightarrow {e}\Big|=\Big|\overrightarrow {ON}\cdot\overrightarrow {OE}\Big|\in\left[\dfrac {\sqrt 3}2,\sqrt 3\right].$$综上知，所求取值范围为 $\left[\dfrac{\sqrt 3}2,\sqrt 7\right]$．
题目 答案 解析 备注
0.113020s