已知函数 $f(x)=\begin{cases} ax^2+x,&x\geqslant 0,\\ -ax^2+x,&x<0,\end{cases}$ 当 $x\in\left[-\dfrac 14,\dfrac 14\right]$ 时恒有 $f(x+a)<f(x)$，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac{1-\sqrt{17}}4,0\right)$
【解析】
显然 $a\neq 0$，接下来按 $a$ 和 $0$ 的大小关系分类讨论．
情形一 $a>0$．
此时 $f(x)$ 单调递增，有 $f(x+a)>f(x)$，不符合题意．
情形二 $a<0$．
此时函数图象如图所示．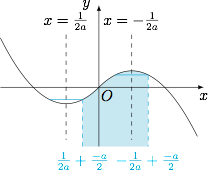
由于不等式 $f(x+a)<f(x)$ 中两个函数值对应的自变量相差为 $-a$，因此用弦长为 $-a$ 的线段"削峰填谷"，可得$$\left[-\dfrac 14,\dfrac 14\right]\subseteq \left(\dfrac{1}{2a}+\dfrac{-a}2,-\dfrac{1}{2a}+\dfrac{-2a}2\right),$$即$$\dfrac{1}{2a}-\dfrac a2<-\dfrac 14,$$即$$2a^2-a-2<0,$$解得 $\dfrac{1-\sqrt{17}}4<a<0$．
综上所述，实数 $a$ 的取值范围是 $\left(\dfrac{1-\sqrt{17}}4,0\right)$．
此时 $f(x)$ 单调递增，有 $f(x+a)>f(x)$，不符合题意．
此时函数图象如图所示．
由于不等式 $f(x+a)<f(x)$ 中两个函数值对应的自变量相差为 $-a$，因此用弦长为 $-a$ 的线段"削峰填谷"，可得$$\left[-\dfrac 14,\dfrac 14\right]\subseteq \left(\dfrac{1}{2a}+\dfrac{-a}2,-\dfrac{1}{2a}+\dfrac{-2a}2\right),$$即$$\dfrac{1}{2a}-\dfrac a2<-\dfrac 14,$$即$$2a^2-a-2<0,$$解得 $\dfrac{1-\sqrt{17}}4<a<0$．综上所述，实数 $a$ 的取值范围是 $\left(\dfrac{1-\sqrt{17}}4,0\right)$．
题目
答案
解析
备注
